Räta linjens ekvation på Högskoleprovet

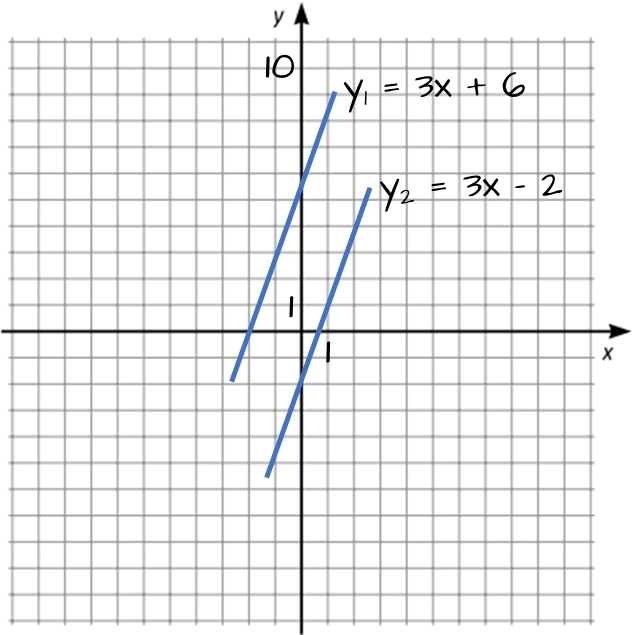
Bestäm riktningskoefficienten och m-värdet för de två linjerna nedan.

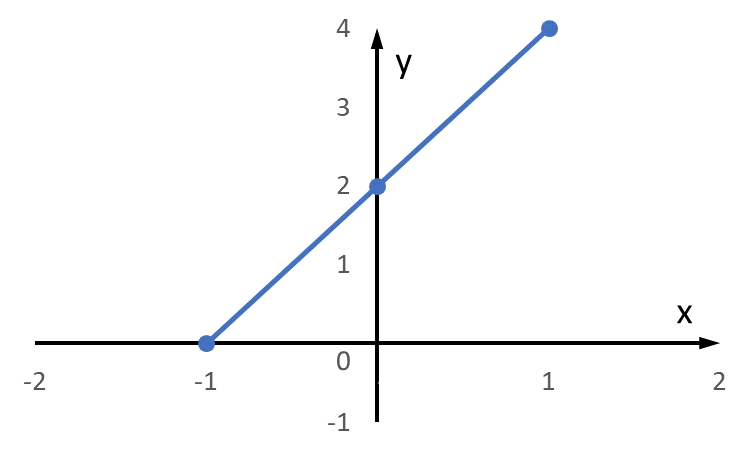
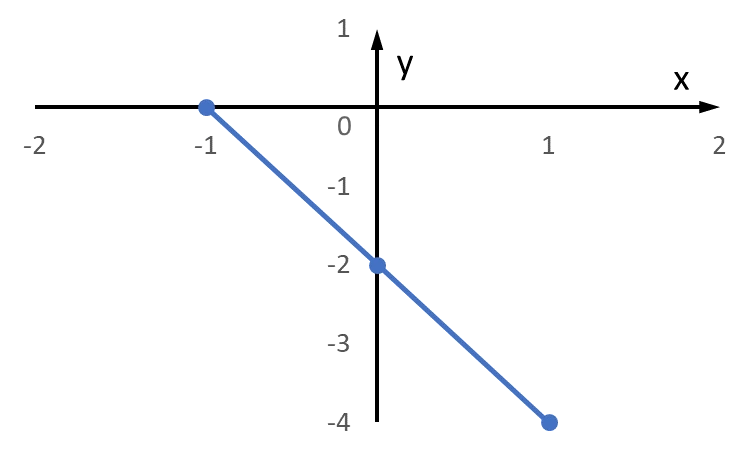
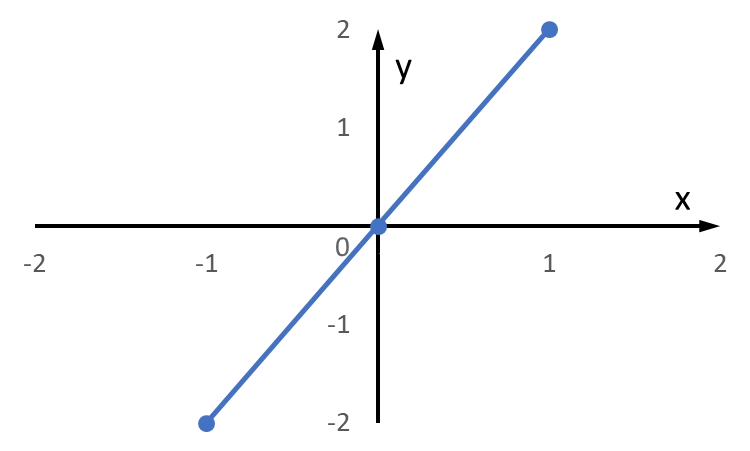
k-värdet kan vi beräkna grafiskt genom att bestämma hur mycket linjen förflyttar sig i y-led för varje förflyttning i x-led. Studerar vi de två linjerna ser vi att för den $f(x)$ är $k=2$ och för $g(x)$ är $k=0,5$. m-värdet är punkten där linjerna skär y-axeln. För $f(x)$ är $m=1$ och för $g(x)$ är $m=-4$.

Ju större riktningskoefficient desto större lutning får alltså linjen. m-värdet talar om för oss hur högt linjen ligger i förhållande till origo.

Svar: För $f(x)$ är k-värdet $2$ och m-värdet är $1.$ För $g(x)$ är k-värdet är $0,5$ och m-värdet är $-4.$

• $k > 0:$ Linjen lutar snett uppåt.
• $m > 0:$ Linjen skär y-axeln ovanför origo.

• $k < 0:$ Linjen lutar snett nedåt.
• $m < 0:$ Linjen skär y-axeln nedanför origo.

• $k > 0:$ Linjen lutar snett uppåt.
• $m = 0:$ Linjen går genom origo.

• $k = 0:$ Linjen är horisontell och parallell med x-axeln.
• $y = 2$ för alla värden på $x.$

• Linjen är vertikal och parallell med y-axeln. För vertikala linjer finns inget k-värde.
• $x = 1$ för alla värden på $y.$

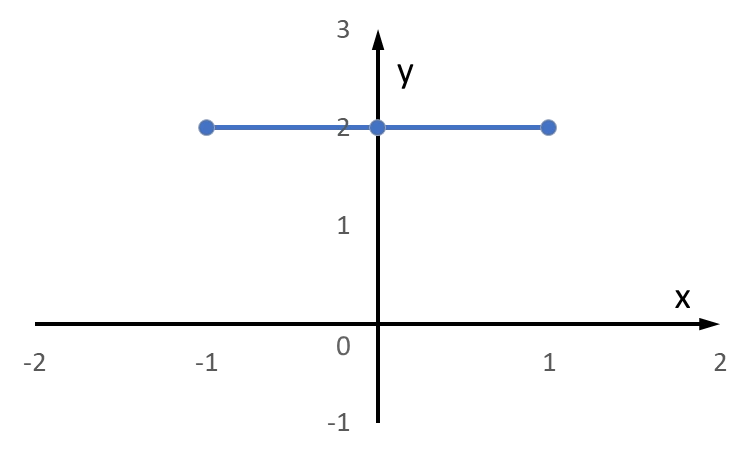
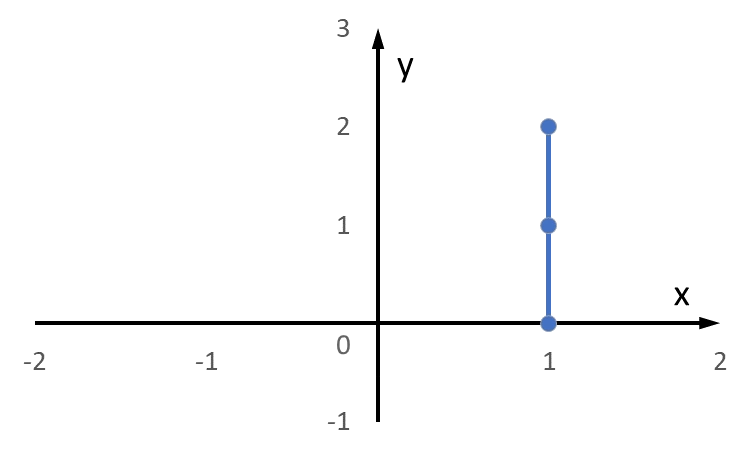
En rät linje passerar genom punkterna $P_1 = (0, -2)$ och $P_2 = (1, 1).$ Vad är linjens ekvation?

Riktningskoefficienten $k$ bestäms genom formeln:

$k=\frac{y_2-y_1}{x_2-x_1}$

Med $P_1$ och $P_2$ insatt får vi:

$k=\frac{1--2}{1-0}=3$

m-värdet får vi givet i punkten $P_1$ då $m$ är lika med y-värdet där $x = 0,$ dvs $m = -2.$

Svar: Linjens ekvation är $y=3x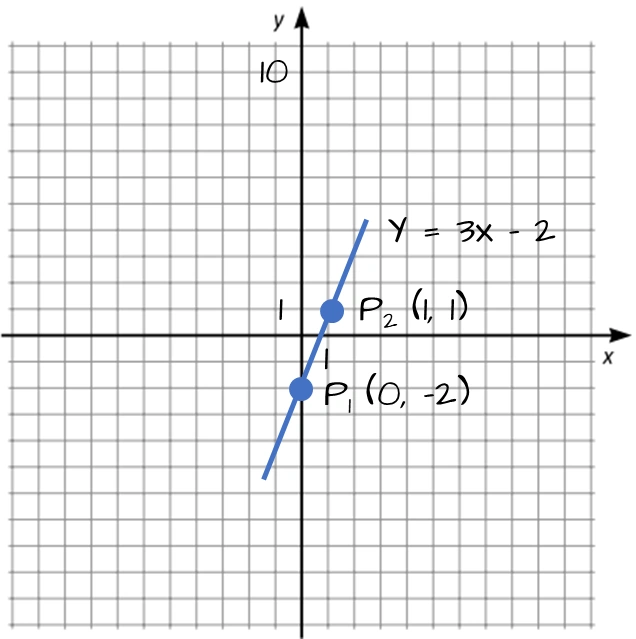 - 2.$

En linje har ekvationen $y = 3x + 3.$ Bestäm koordinaterna för var linjen skär x-axeln respektive y-axeln.

För att hitta skärningspunkten med x-axeln sätter vi $y = 0:$ $3x + 3 = 0,$ vilket ger $x = -1.$ Skärningspunkten med x-axeln är alltså $(-1, 0).$

För att hitta skärningspunkten med y-axeln sätter vi $x = 0:$ $y = 3 \cdot 0 + 3,$ vilket ger $y = 3.$ Skärningspunkten med y-axeln är alltså $(0, 3).$ Notera att y-värdet är samma som linjens m-värde.

Svar: Linjens skärningspunkt med x-axeln är $(-1, 0)$ och med y-axeln $(0, 3).$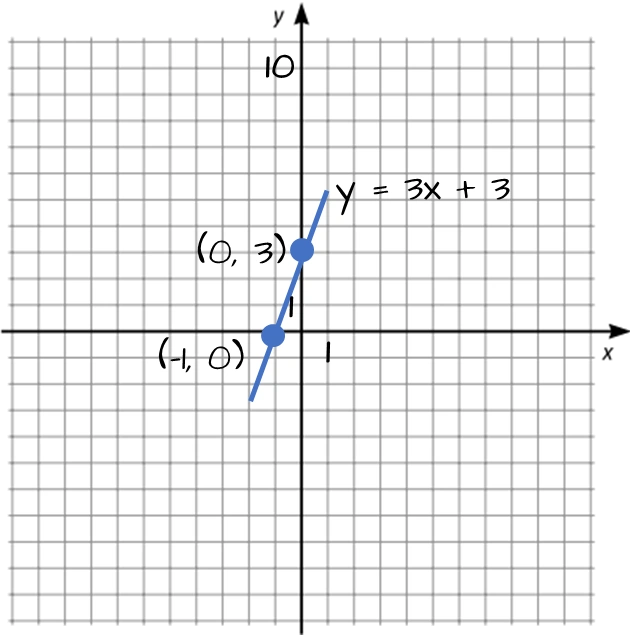

En linje har riktningskoefficienten $-2$ och går genom punkten $(1, 2).$ Bestäm linjens ekvation.

Vi sätter in de värden vi har i enpunktsformeln

$y-2=-2(x-1) \Rightarrow y-2=-2x+2$

$\Rightarrow y=-2x+4$

Svar: Linjens ekvation är $y = -2x + 4$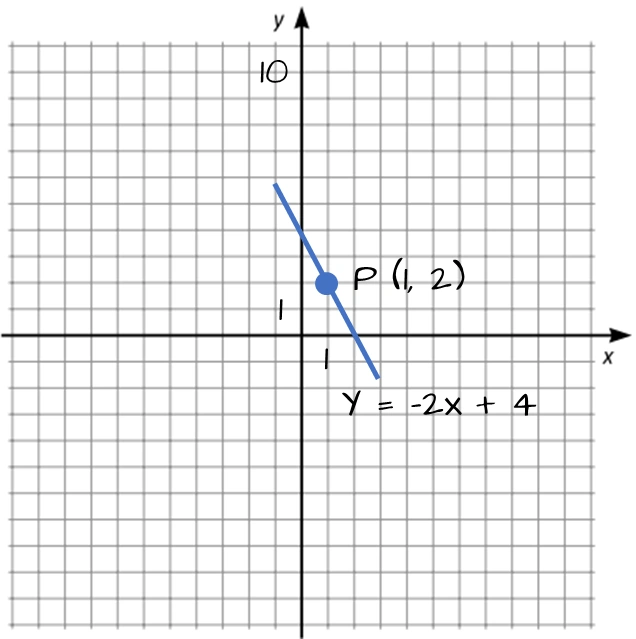

Temperaturen på 20 meter över havet (m.ö.h.) är 20°C. Temperaturen faller linjärt med ökad höjd och är 10°C vid höjden 1 000 m.ö.h.

1. Beskriv höjden som en ekvation av temperaturen.
2. Vid vilken höjd är temperaturen noll grader?

Låt $x$ beteckna temperaturen i °C och $y$ höjden i meter. Sambandet skrivs $y = kx + m.$ Av texten får vi då två punkter:

• $P_1 = (20, 20)$
• $P_2 = (10, 1000)$

Med två punkter kan vi använda oss av formeln för att beräkna k-värdet:

$k=\frac{1000-20}{10-20}= -98$.

Vi sätter in $P_1$ och k-värdet i enpunktsformeln och löser ut:

$y - 20 = -98(x-20) \Rightarrow y = -98x + 1980.$

Sätter vi $x = 0$ i vår ekvation får vi höjden $y = 1980\, m.$

Svar: A. Ekvationen är $y = -98x + 1980,$ där $x$ är temperaturen och $y$ är höjden. B. Vid $1980$ m är temperaturen

Bestäm konstanten $\boldsymbol{a}$ i ekvationen $\boldsymbol{y_1 - ax - 6 = 0}$ så att motsvarande linje är parallell med linjen $\boldsymbol{y_2 - 3x + 2 = 0.}$

Ekvationerna i texten är skrivna på allmän form. Att en ekvation är skriven på allmän form förekommer ibland på Högskoleprovet och vi behöver skriva om dessa:

• Vår första linje är: $y_1 - ax - 6 = 0.$
  $y_1 = ax + 6$
• Vår andra linje är: $y_2 - 3x + 2 = 0$
  $y_2 = 3x - 2$

Nu är ekvationerna för våra linjer skrivna på k-form. Vi vet att då två linjer är parallella har de samma k-värde och vi kan dra slutsatsen att $a = 3.$

Svar: $a = 3$

$f(x) = 2x + 4.$ $g(x)$ är vinkelrät mot $f(x).$ $g(x)$ passerar genom punkten $(4, 0).$ Vad är $\boldsymbol{g(x)?}$

Då två linjer är vinkelräta gäller $k_1 \cdot k_2=-1$. Eftersom $f(x)$ har k-värdet $2$ gäller alltså $2 \cdot k_2=-1,$ vilket ger $k_2=-\frac{1}{2}$.

$g(x) = -\frac{x}{2} + m$

Enligt texten ska $g(x)$ passera genom punkten $(4,0),$ dvs. $g(4) = 0:$

$g(4) = 0 \Leftrightarrow -\frac{4}{2} + m = 0 \Rightarrow m = 2$.

Svar: $g(x) = -\frac{x}{2} + 2$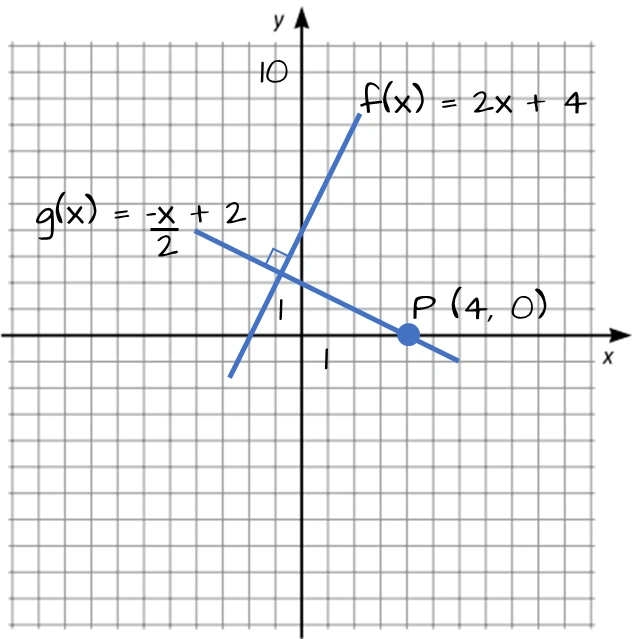

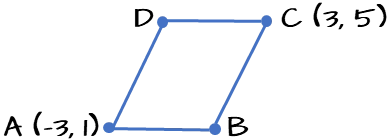
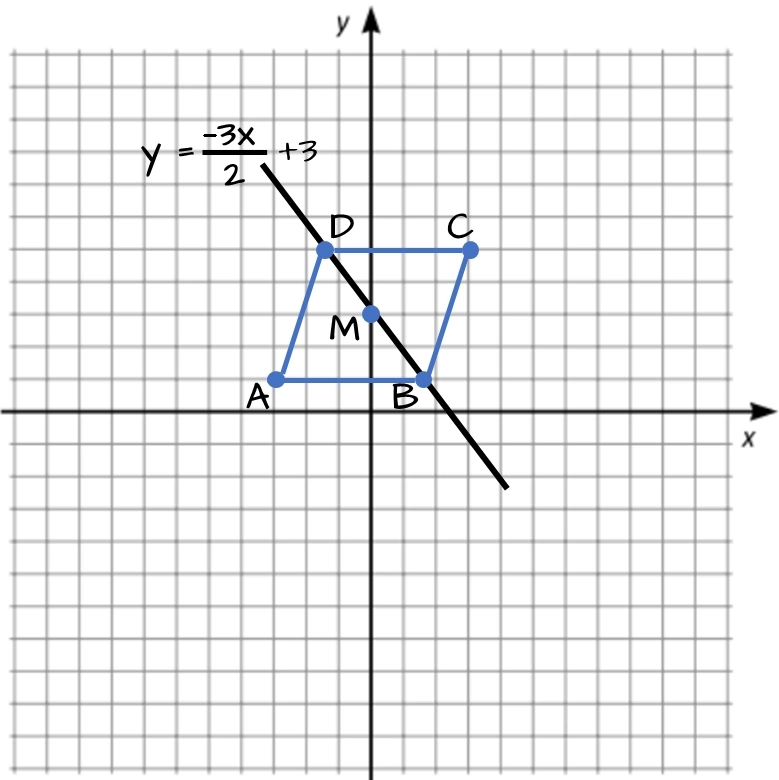
$A(-3,1)$ och $C(3,5)$ är två av hörnen i romben $ABCD.$

Vad är ekvationen för linjen som går genom punkterna $\boldsymbol{B}$ och $\boldsymbol{D?}$

Lösningsförslag 1:
Studerar vi figuren, ser vi att linjen vi söker, som vi kallar $y_{BD}$ har negativ riktningskoefficient (lutar snett nedåt) vilket gör att vi kan förkasta svarsalternativen A och C. Vi ser också att y-värden för romben är positiva. Därmed vet vi att $y_{BD}$ kommer att skära y-axeln ovanför origo, vilket ger ett positivt m-värde. Vi kan därför även utesluta svarsalternativet D och vi vet då att B är rätt svar.

Lösningsförslag 2:
En romb är en parallellogram, vilket innebär att diagonalerna halverar varandra. Diagonalerna $AC$ och $BD$ skär därför varandra i rombens mittpunkt $M(x_M,y_M).$ Dessutom är diagonalerna i en romb vinkelräta mot varandra. Det kan vi utnyttja för att bestämma linjen genom $B$ och $D.$

$x_M = \frac{x_A+x_C}{2}=\frac{-3+3}{2}=0$

$y_M = \frac{y_A+y_C}{2}=\frac{1+5}{2}=3$

Rombens mittpunkt $M$ är alltså $(0,3)$ och vi har en punkt på $y_{BD}.$ Med hjälp av våra punkter $A$ och $C$ beräknar vi riktningskoefficienten för $y_{AC}:$

$k_{AC}=\frac{y_C-y_A}{x_C-x_A}=\frac{5-1}{3--3}=\frac46=\frac23$

Nu har vi det vi behöver för att beräkna riktningskoefficienten för $y_{BD}$ som alltså är vinkelrät mot $y_{AC}:$

$k_{BD}=\frac{-1}{k_{AC}}=-\frac32$

I det här exemplet behöver vi inte använda enpunktsformeln, då vi fick linjen $y_{BD}$ skärning med y-axeln gratis då vi beräknade punkten $M$:

$y_{BD}=-\frac{3}{2}x+3$

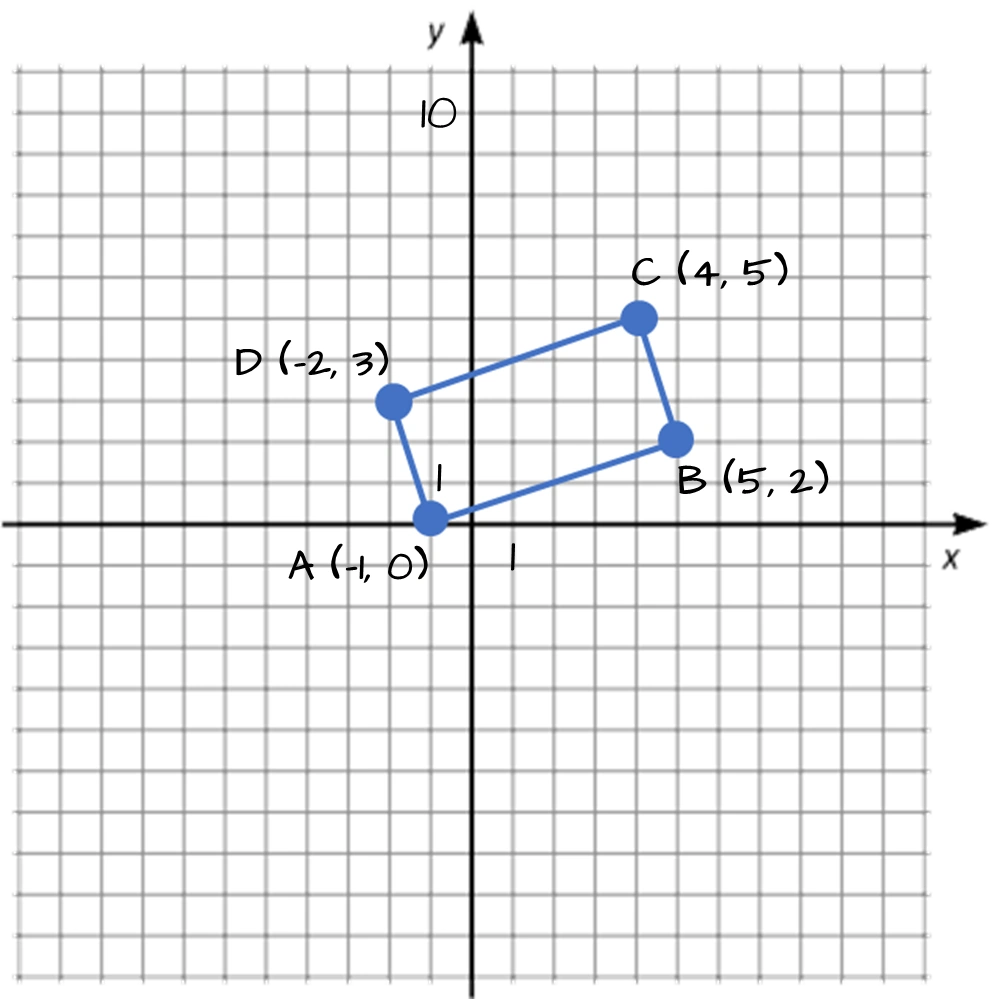
Representerar koordinaterna $\boldsymbol{A(-1 , 0),}$ $\boldsymbol{B(5 , 2),}$ $\boldsymbol{C(4 , 5)}$ och $\boldsymbol{D(-2 , 3)}$ hörnen av en rektangel?

En rektangel har följande egenskaper:

• Motstående sidor är parallella och lika långa.
• Närliggande sidor är vinkelräta.

Låt oss testa om koordinaterna uppfyller egenskaperna för en rektangel. Vi börjar med att beräkna lutningen för att se om sidorna är parallella.

Lutningen $k$ ges av formeln: $$k=\frac{y_2-y_1}{x_2-x_1}$$

• $k_{AB}=\frac{2-0}{5-(-1)}=\frac26=\frac13$
• $k_{BC}=\frac{5-2}{4-5}=-3$
• $k_{CD}=\frac{3-5}{-2-4}=\frac13$
• $k_{DA}=\frac{0-3}{-1-(-2)}=-3$

Sidorna $AB$ och $CD$ är parallella med lutningen $\frac13$ och sidorna $BC$ och $DA$ är parallella med lutningen $-3.$

För att beräkna om sidorna är lika långa använder vi avståndsformeln: $$\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$

• Längd$_{AB}= \sqrt{(5-(-1))^2+(2-0)^2}=\sqrt{40}$
• Längd$_{BC}= \sqrt{(4-5)^2+(5-2)^2}=\sqrt{10}$
• Längd$_{CD}= \sqrt{(-2-4)^2+(3-5)^2}=\sqrt{40}$
• Längd$_{DA}= \sqrt{(-1-(-2))^2+(0-3)^2}=\sqrt{10}$

Längden på rektangelns bas $= \sqrt{40}$ längdenheter och höjd $= \sqrt{10}$ längdenheter.

För att testa om närliggande sidor är vinkelräta beräknar vi produkten av respektive linjes k-värde. Vi vet att två linjer är vinkelräta om produkten av respektive linjes k-värde $= -1.$

$k_{AB} \cdot k_{BC} = \frac13 \cdot -3 = -1$

$k_{CD} \cdot k_{DA} = \frac13 \cdot -3 = -1$

Vi kan konstatera att de närliggande sidorna är vinkelräta och därmed är alla egenskaper för rektangeln uppfyllda.

Svar: Ja, koordinaterna representerar hörnen i en rektangel.