Likformighet på Högskoleprovet

Sammanfattning Likformighet på Högskoleprovet

Två objekt är likformiga om:

Vinklarna i det ena objektet är lika stora som vinklarna i det andra objektet.
och/eller om förhållandet mellan motsvarande sidor i objekten är detsamma.

I likformiga trianglar är förhållandet mellan motsvarande sidor lika.

Fig. 1

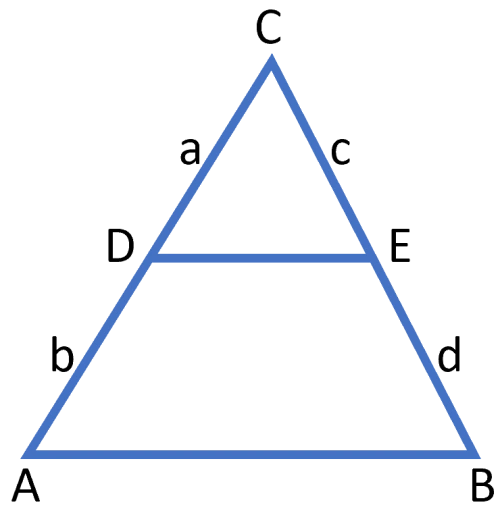Fig. 2

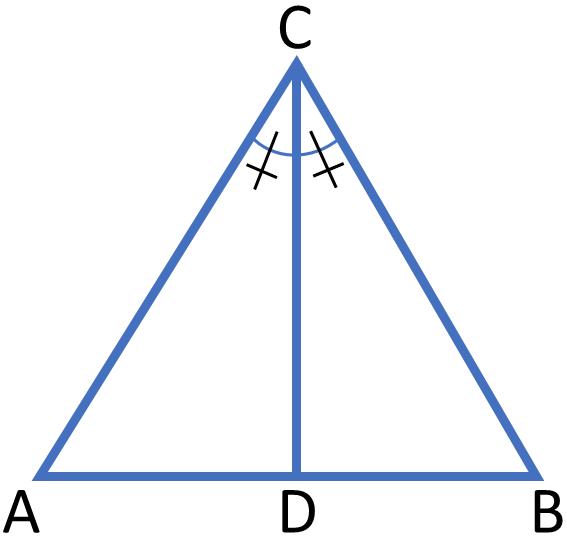Fig. 3

Topptriangelsatsen (Fig 1) $\frac{a}{b}=\frac{c}{c+d}$
Transversalsatsen (Fig 2) $\frac{a}{b}=\frac{c}{d}\;\;eller\;\;\frac{b}{a}=\frac{d}{c}$
Bisektrissatsen (Fig 3) $\frac{AD}{BD}=\frac{AC}{BC}$

Likformighet och avbildningar

För uppgifter med likformighet kan det vara bra att tänka på avbildningar eller kartor. Att två geometriska figurer (t.ex. trianglar) är likformiga betyder att de har exakt samma form, men inte nödvändigtvis samma storlek. Vi kan dra slutsatsen att två objekt är likformiga om:

Vinklarna i det ena objektet är lika stora som vinklarna i det andra objektet
och/eller om förhållandet mellan motsvarande sidor i objekten är detsamma.

Två objekt som har samma storlek och form, men kan vara olika orienterade är kongruenta.

Exempel: Likformighet 1

Trianglarna $ABC$ och $DEF$ är likformiga. Bestäm sträckan $\boldsymbol{x.}$

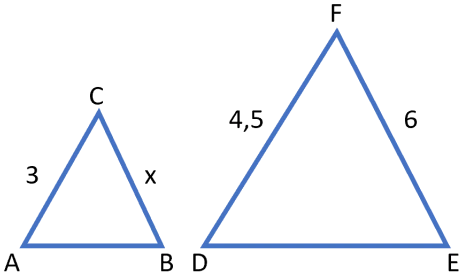
exempel1-likformighet

Vi vet att i likformiga trianglar är förhållandet mellan motsvarande sidor lika, dvs

$\frac{AC}{DF}=\frac{BC}{EF}$

$\frac{3}{4,5}=\frac{x}{6}$

Korsvis multiplikation ger:

$x=\frac{6 \cdot 3}{4,5}=\frac{18}{4,5}=4$

Svar: Sträckan $x = 4$ längdenheter.

Exempel: Likformighet 2

Trianglarna $ABC$ och $DEF$ är likformiga. Bestäm vinkeln $\boldsymbol{y.}$

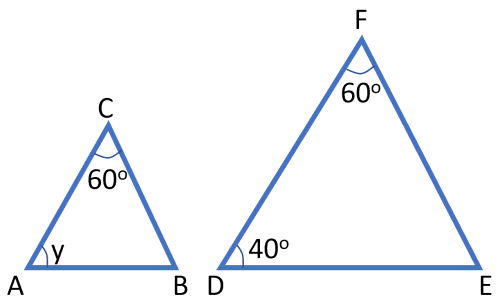
exempel2 likformighet

Vi vet att i likformiga trianglar är vinklarna i den ena triangeln lika stora som vinklarna i den andra triangeln, dvs.

Vinkeln $y =$ vinkeln $EDF = 40^o.$

Svar: Vinkeln $y = 40^o.$

Exempel: Likformighet 3

Vad är arean $\boldsymbol{A?}$

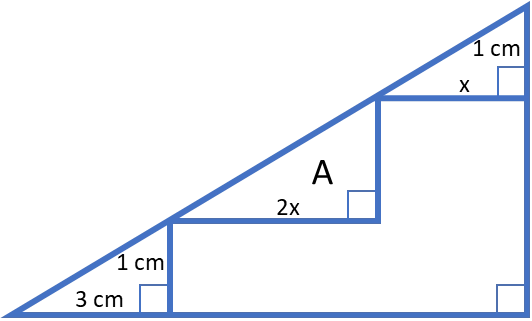
exempel4 likformighet

Vi kallar höjden i den stora triangeln $y$. Förutom triangeln $A$ med basen $2x$ och höjden $y-2$ kallar vi:

Den stora triangeln $T_1$ som har basen $3+3x$ och höjden $y.$
och den lilla triangeln $T_3$ med basen $3\,cm$ och höjden $1\,cm.$

$A, T_1$ och $T_2$ är likformiga, dvs förhållandena mellan respektive triangels bas och höjd är samma. Det här ger oss:

$T_1$ är likformig med $T_3$: $\frac{y}{3+3x}=\frac13$
$A$ är likformig med $T_3$: $\frac{y-2}{2x}=\frac13$

Ekvation 1 ger: $y=x+1$ insatt i ekvation 2:

$\frac{x+1-2}{2x} = \frac13$

$3x-3=2x$

$x=3$ vilket ger $y=4$

$A$ har basen $2x = 6\,cm$ och höjden $y-2=2\,cm$

Arean $A=\frac{6\cdot2}{2}=6\,cm^2$

Svar: Arean $A = 6\, cm^2$

Exempel: Likformighet 4

Vad är arean $\boldsymbol{A?}$

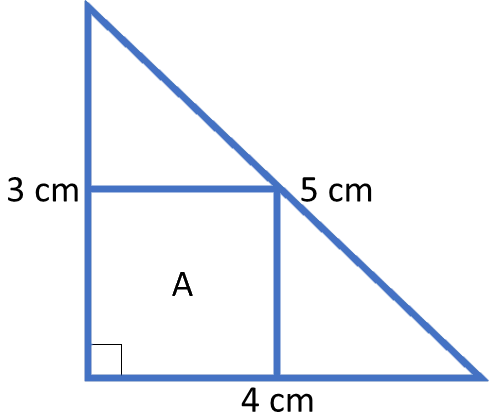
exempel5 likformighet

Vi kallar sidorna i kvadraten $a.$ Den inskrivna kvadraten bildar två mindre trianglar. Båda dessa trianglar är likformiga med den stora triangeln. Triangeln närmast basen i triangeln har basen $(4 - a)$ och höjden $a.$

Förhållandet mellan dessa är lika med förhållandet mellan den stora triangelns bas och höjd:

$\frac{4-a}{a}=\frac43 \Rightarrow 3(4-a) = 4a$

$12-3a = 4a \Rightarrow a = \frac{12}{7} \,cm.$

Arean $A = (\frac{12}{7})^2 = \frac{144}{49}\,cm^2$

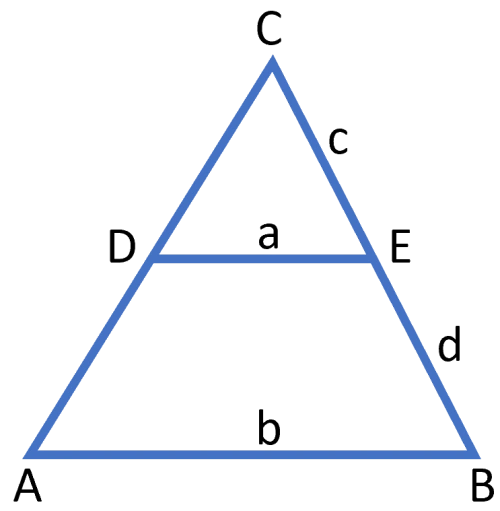
Svar: Arean $A = \frac{144}{49}\, cm^2$

Topptriangelsatsen

Topptriangelsatsen säger att den topptriangel (CDE i figuren nedan) som bildas av en sk parallelltransversal ($DE$ i figuren) är likformig med hela triangeln ($ABC$ i figuren nedan).

En parallelltransversal är alltså en linje som skär två sidor och är parallell med den tredje.

$$\frac{a}{b}=\frac{c}{c+d}$$

topptriangelsatsen

Exempel: Topptriangelsatsen

$DE$ är parallell med $AB.$ Beräkna längden $\boldsymbol{x}$ i triangel $\boldsymbol{ABC.}$

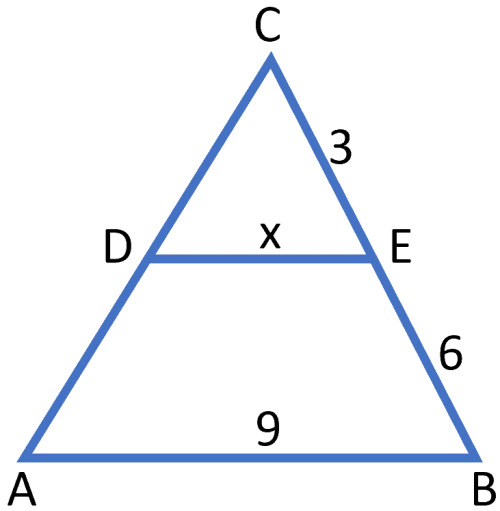
exempel-topptriangelsatsen2

Enligt topptriangelsatsen är $CDE$ likformig med triangeln $ABC,$ dvs:

$\frac{x}{9}=\frac{3}{3+6}$

$\Rightarrow x=9 \cdot \frac{3}{9}$

$\Rightarrow x = 3$ längdenheter

Svar: $x = 3$ längdenheter

Transversalsatsen

Transversalsatsen säger att en parallelltransversal som delar två sidor av en triangel, delar dessa båda sidor i samma förhållande, dvs:
$$\frac{a}{b}=\frac{c}{d}\;\;eller\;\;\frac{b}{a}=\frac{d}{c}$$

transversalsatsen

Exempel: Transversalsatsen

$DE$ är parallell med $AB.$ Beräkna längden $\boldsymbol{x.}$

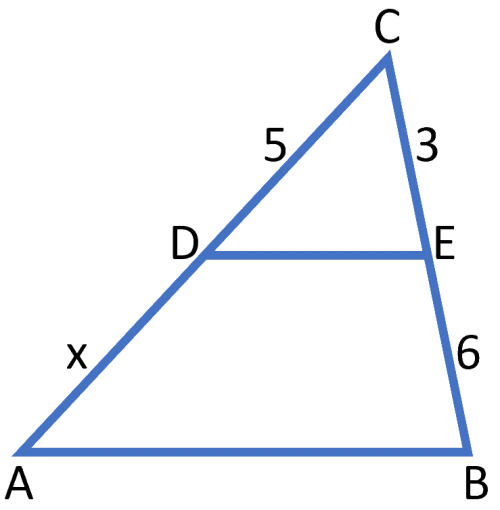
exempel-transversalsatsen

Enligt transversalsatsen:

$\frac{x}{5}=\frac{6}{3}$

$x=\frac{5 \cdot 6}{3}=10$

Svar: $x = 10$ längdenheter

Bisektrissatsen

En bisektris är en linje som delar en vinkel mitt itu. Vi använder symbolen symbol-lika-vinkel för att indikera att de två vinklarna är lika.

bisektrissatsen

Bisektrissatsen säger att en bisektris i en triangel delar den mot vinkeln motstående sidan enligt följande förhållande: $$\frac{AD}{BD}=\frac{AC}{BC}$$

Exempel: Bisektrissatsen

Beräkna längden $\boldsymbol{x.}$

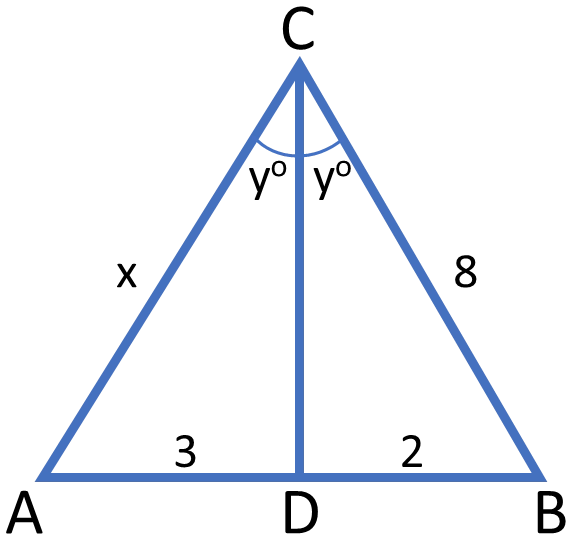
exempel-bisektrissatsen

Enligt bisektrissatsen:

$\frac32=\frac{x}{8}$

$x=\frac{8 \cdot 3}{2}=12$

Svar: $x = 12$ längdenheter

Längdskala, areaskala och volymskala

Skalor beskrivs i avsnittet Omkrets, area och volym. Vid avbildningar och likformighet beskriver skalor förhållanden mellan längd, area och volym. Förhållandet mellan längdskala, areaskala och volymskala definieras enligt följande: $$areaskala = (längdskala)^2$$ $$volymskala = (längdskala)^3$$

Exempel: Areaskala

Arean $T1 = 12\, cm^2.$ Bestäm arean $\boldsymbol{T2.}$

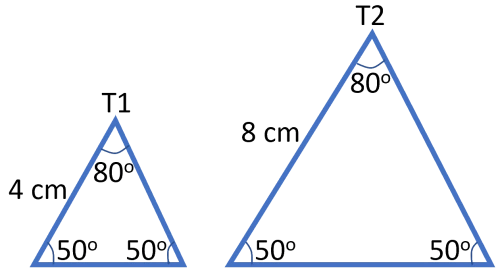
exempel-areaskala

Eftersom vinklarna i $T1$ är lika med vinklarna i $T2$ vet vi att $T1$ och $T$2 är likformiga.

Längdskalan $= \frac{Sidan \: T2}{Sidan \: T1}=\frac84 = 2$

areaskalan $=$ (längdskala)$^2 = 2^2 = 4$

Arean $T2 =$ areaskalan $\cdot$ arean $T1 = 4 \cdot 12\, cm^2 = 48\, cm^2$

Svar: Arean $T2 = 48\, cm^2$