HÖGSKOLEPROVET
| ton | kg | hg | g |
|---|---|---|---|
| 1 ton | 1 000 | 104 | 106 |
| 1 kg | 10 | 1 000 | |
| 1 hg | 100 |
Skriv dessa vikter i kilogram (kg):
| mil | km | m | dm | cm | mm |
|---|---|---|---|---|---|
| 1 mil | 10 | 104 | 105 | 106 | 107 |
| 1 km | 1 000 | 104 | 105 | 106 | |
| 1 m | 10 | 100 | 1 000 | ||
| 1 dm | 10 | 100 | |||
| 1 cm | 10 |
Skriv dessa längder i meter (m):
Formeln för hastighet är: $$sträckan=tiden \cdot hastigheten$$ Genom att enbart titta på enheten för hastighet, km/h, kan vi härleda formeln utan att behöva memorera. Enheten för sträcka = km och enheten för tid = h. Därmed vet vi att $$hastighet\: [km/h] = \frac{sträcka \: [km]}{tid \: [h]}$$
Ibland mäter vi hastigheten i andra enheter, tex. meter per sekund, m/s. Att omvandla km/h till m/s kan vi också göra enbart genom att studera enheterna. Vi vet att 1 kilometer = 1 000 m och att 1 h = 60 minuter = (60 · 60) sekunder = 3 600 sekunder. Det här ger: $$km/h = \frac{1\;000 \: [m]}{3\;600 \: [s]}=\frac{1 [m]}{3,6 [s]}$$ Dvs. 1 km/h motsvarar ca. 0,28 m/s och omvänt 3,6 km/h motsvarar 1 m/s.
En båt kör med hastigheten 54 km/h. På sjön mäts hastigheten oftast i knop. 1 knop ≈ 0,5 m/s. Uttryck båtens hastighet i knop.
Vi börjar med att omvandla hastigheten till m/s.
54 km/h = $\frac{54\;000 \: m}{60 \cdot 60 \: s}=\frac{54 \: m}{3,6 \:s}=$ 15 m/s
15 m/s omvandlat till knop ≈ $\frac{15}{0,5}$ ≈ 30 knop.
Hastigheten på en 10 mil lång motorväg sänks från 120 km/h till 100 km/h. Förutsatt att trafikanterna håller hastighetsbestämmelserna, vad innebär hastighetsförändringen i tidsförändring på en timma?
Tiden det tar att köra 100 km med medelhastigheten 100 km/h = $\frac{100 \: km}{100 \: km/h}=$ 1 h.
Tiden det tar att köra 100 km med medelhastigheten 120 km/h=
$\frac{100\: km}{120 \: km/h}=\frac56 \: h= \frac56 \cdot 60$ minuter = 50 minuter
Tidsökningen är således (60 - 50) minuter = 10 minuter.
Då två objekt rör sig i samma riktning är deras relativa hastighet differensen mellan respektive objekts hastighet.
Ett tåg på den röda linjen passerar ett tåg på den blå linjen på 15 sekunder. Tåget på den röda linjen har hastigheten 72 km/h och tåget på den blå linjen hastigheten 54 km/h. Hur långt är tåget på röd linje?
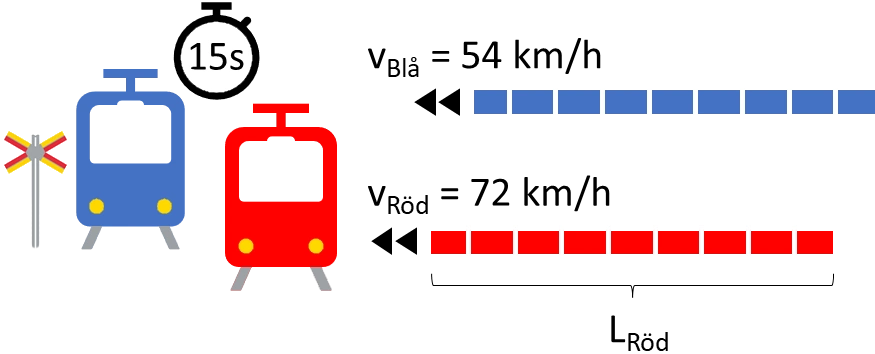
Vi kallar tågets hastighet på den röda linjen vRöd = 72 km/h och på den blå linjen vBlå = 54 km/h. Längden av tåget på den röda linjen kallar vi LRöd:
$L_{Röd} = (v_{Röd} - v_{Blå}) \cdot \frac{1000\text{ m}}{3600\text{ s}} \cdot 15 \text{ s} = 75 \text{ m.}$
Svar: 75 meter.
Då två objekt rör sig i motsatt riktning är deras relativa hastighet summan av respektive objekts hastighet.
Två tåg startar samtidigt och färdas mot samma punkt. Det ursprungliga avståndet mellan tåget är 900 km. Respektive tågs hastighet är 156 km/h respektive 144 km/h.
Efter hur lång tid möts tågen?
Vi kallar tågen A respektive B. Hastigheten vA = 156 km/h och vB = 144 km/h. Tiden till tågen möts = t:
$t(156+144) \text{ km/h} = 900 \text { km} \Rightarrow 300t = 900$
$\Rightarrow t = 3 \text{ h.}$
Svar: 3 timmar.
Då ett objekt i rörelse, exempelvis ett tåg med längden lt och hastigheten vt, passerar ett stillastående objekt, exempelvis en plattform med längden lp, så är tiden det tar för tåget att passera plattformen lika med:
$\frac{l_t+l_p}{v_t}$
Vad är tiden för ett godståg med längden 120 meter och hastigheten 72 km/h att passera en plattform med längden 260 meter?
Vi kallar tågets längd = lt = 120 m. och tågets hastighet = vt = 72 km/h. Plattformens längd kallar vi lp = 260 m.
Tiden det tar för tåget att passera plattformen =
$\frac{l_t+l_p}{v_t}=\frac{120+260\text{ m}}{72 \text{ km/h}}=$
$=\frac{120+260\text{ m}}{\frac{72 \cdot 1000}{60\cdot60}}=$
$=\frac{380}{20}=19 \text{ sekunder}$
Svar: 19 sekunder.
Då vi arbetar med uppgifter som består av att beräkna tiden det tar för två objekt att mötas då de startar vid samma punkt, men håller olika hastighet, använder vi oss av minsta gemensamma multipel. En gemensam multipel till två heltal är ett tal som är en multipel av vart och ett av talen. Multiplar av 3 är 3, 6, 9, 12, 15, 18, 21, 24, ... och multiplar av 8 är 8, 16, 24, ... Minsta gemensamma multipel av 3 och 8 är alltså 24.
Kalle och Simon startar från samma punkt och går i samma riktning runt en 120 meter lång, cirkulär bana. Kalle håller den konstanta hastigheten 12 m/min och Simon 20 m/min. Efter hur lång tid möts de två vid startpunkten igen?
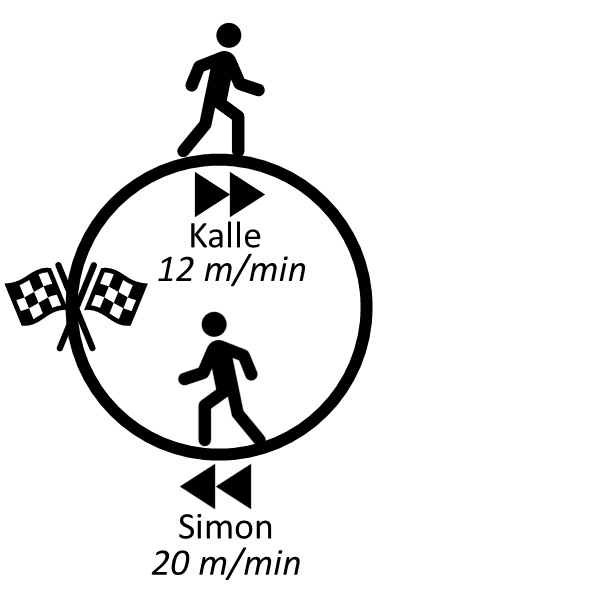
Tiden efter att Kalle och Simon möts får vi om vi beräknar minsta gemensamma multipel av tiden det tar för de två att gå ett varv runt banan.
Tiden det tar för Kalle att gå ett varv = $\frac{120}{12}=10\,\,minuter$ och för Simon = $\frac{120}{20}=6\,\,minuter$. Minsta gemensamma multipel av 10 och 6 är 30.
Svar: Kalle och Simon möts igen vid startpunkten efter 30 minuter.
Två satelliter med omloppstiderna 90 minuter respektive 150 minuter passerar en punkt på jorden samtidigt. Efter hur lång tid kan vi se satelliterna igen?
Vi börjar med att primtalsfaktorisera omloppstiderna:
90 minuter = $2 \cdot 3 \cdot 3 \cdot 5$ minuter.
160 minuter = $2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 5$ minuter.
Gemensamma faktorer av omloppstiderna är 5 och 2 och vi för in tiderna i ett venndiagram. Den vänstra cirkeln och snittet motsvarar faktorerna i A:s omloppstid och motsvarande för B och den högra cirkeln och snittet:
Tiden till vi ser satelliterna igen får vi om vi multiplicerar faktorerna i venndiagrammet =
$3 \cdot 3 \cdot 5 \cdot 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2$ = 1440 minuter = 24 timmar.
Svar: Tiden till vi ser satelliterna igen är 24 timmar.
På Högskoleprovet får vi ibland uppgifter om tid och arbete. Om vi antar att person A kan utföra en viss mängd arbete på x dagar, så är arbetet denne utför per dag = $\frac{1}{x}$. Omvänt gäller att om $\frac{1}{x}$ mängd arbete utförs per dag så kommer det att ta x dagar för hela arbetet att utföras. Om personen A utför en viss del av arbetet, exempelvis $\frac{1}{d}$ av arbetet, på t timmar så kommer det att ta dt timmar att utföra hela arbetet.
Om två personer A och B hjälps åt att utföra ett arbete och A utför $\frac{1}{x}$ del av arbetet per dag och B utför $\frac{1}{y}$ del av arbetet per dag så kommer de att gemensamt utföra $\frac{1}{x} + \frac{1}{y}$ delar av arbetet per dag.
Adam målar en vägg på 12 dagar och Bertil målar samma vägg på 15 dagar. Hur lång tid tar det att måla väggen om Adam och Bertil målar väggen tillsammans?
Adam målar $\frac{1}{12}$ av väggen per dag och Bertil målar $\frac{1}{15}$ av väggen per dag. Tillsammans målar Adam och Bertil $\frac{1}{12}+\frac{1}{15}=\frac{9}{60}=\frac{3}{20}$ av väggen per dag.
Tiden det tar för Adam och Bertil att tillsammans måla hela väggen = $\frac{1}{\frac{3}{20}}=\frac{20}{3}=\,6\frac23\,\,dagar$
Svar: Det tar $\,6\frac23\,\,dagar$ för Adam och Bertil att måla väggen tillsammans.
Adam och Bertil målar tillsammans en vägg på 15 dagar. Om Bertil skulle måla väggen själv skulle det ta 20 dagar. Hur lång tid tar det för Adam att själv måla väggen?
På en dag målar Adam och Bertil $\frac{1}{15}$ av väggen och Bertil målar $\frac{1}{20}$ av väggen. Andelen av väggen som Adam målar är då $\frac{1}{15}-\frac{1}{20}=\frac{4-3}{60}=\frac{1}{60}$ per dag och det skulle således ta 60 dagar för Adam att måla väggen själv.
Svar: Det skulle ta Adam 60 dagar att själv måla väggen.
Det tar 7 dagar för fyra identiska maskiner att tillsammans utföra en viss uppgift. Hur många fler sådana maskiner behövs för att samma uppgift ska utföras på 4 dagar?
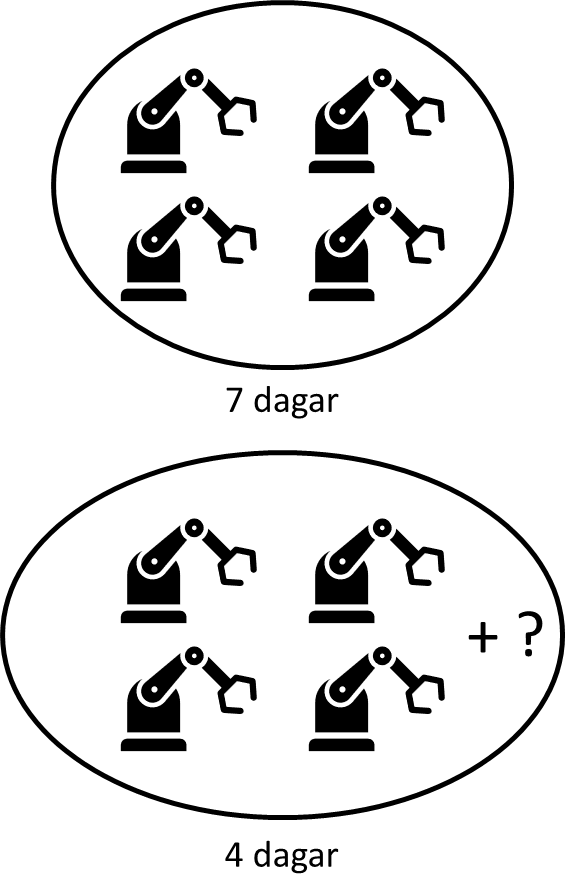
Arbetet som ska utförs av 4 maskiner kan vi skriva som ekvationen $A = 4r \cdot 7\,dagar$ där A är arbetet som ska utföras och r är hastigheten med vilken varje maskin arbetar.
Vi adderar nu n maskiner för att utföra samma uppgift och skriver denna ekvation $A = (4+n)r \cdot 4\,dagar$. Då det är samma arbete som ska utföras sätter vi våra ekvationer lika med varandra:
$4r \cdot 7 = (4+n)r \cdot 4$
Vi kan förkorta bort r från varje led:
$28 = 16 + 4n \Rightarrow 4n = 12 \Rightarrow n = 3$
Svar: 3 fler maskiner behövs för att utföra uppgiften på 4 dagar.
Vi kan mäta hastighet på många olika sätt. I uppgifter om en viss volym per tidsenhet går vi tillväga på motsvarande sätt som tidigare. Om vi tänker oss tiden det tar att fylla upp en viss volym av en flaska med en kran som spolar med en viss volym per timma, så är tiden lika med volymen av flaskan dividerat med den vattenvolym som kranen spolar per timma.
För att fylla ett badkar spolas vatten från kallvattenkranen, varmvattenkranen och duschen. Tiden för att fylla badkaret enbart med kallvattenkranen är 12 minuter, med varmvattenkranen 20 minuter och med duschen 30 minuter. Om samtliga kranar och duschen samtidigt spolar, hur lång tid tar det för badkaret att fyllas?
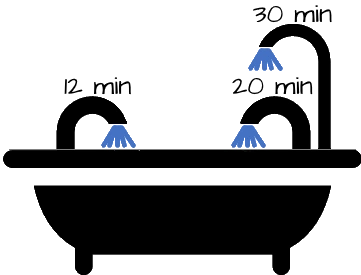
Kallvattnet fyller $\frac{1}{12}$ av badkaret per minut, varmvattnet fyller $\frac{1}{20}$ av badkaret per minut och duschen fyller $\frac{1}{30}$ av badkaret per minut.
Tillsammans fylls $\frac{1}{12}+\frac{1}{20}+\frac{1}{30}$ av badkaret per minut. Minsta gemensamma nämnare = 60 och vi gör om de tre bråken till 60-delar för att kunna skriva på gemensamt bråkstreck:
$\frac{1}{12}+\frac{1}{20}+\frac{1}{30}=\frac{5+3+2}{60}=\frac{10}{60}=\frac16$
Hela badkaret fylls på $\frac{1}{\frac16}=6\,\,minuter$
Svar: Det tar 6 minuter att fylla badkaret.
Ett badkar på 500 liter fylls på med 25 liter/minut, men proppen är borta och badkaret töms därför samtidigt med 15 liter/minut. Beräkna tiden till det är fullt.
Tiden till badkaret är fullt = $\frac{500 \text{ liter}}{(25-15)\text{ l/min}}=\frac{500}{10}=$ 50 minuter.
Svar: Det tar 50 minuter att fylla badkaret.
En liten pump fyller en tank på 1 timme. En stor pump fyller samma tank på 15 minuter. Om båda pumparna startas samtidigt, hur lång tid tar det då att fylla tanken?
Den lilla pumpen fyller $\frac{1}{60}$ av tanken på en minut och den stora pumpen $\frac{1}{15}$ av tanken per minut.
Tillsammans fyller de två pumparna $\frac{1}{60}+\frac{1}{15}$ av tanken per minut, vilket är lika med $\frac{1+4}{60}=\frac{5}{60}=\frac{1}{12}$ av tanken per minut.Hela tanken fylls på $\frac{1}{\frac{1}{12}}=12$ minuter.
|
Beteckning Namn Tiopotens |
G giga 109 |
M mega 106 |
k kilo 103 |
h hekto 102 |
d deci 10-1 |
|---|---|---|---|---|---|
|
Beteckning Namn Tiopotens |
c centi 10-2 |
m milli 10-3 |
μ mikro 10-6 |
n nano 10-9 |
p piko 10-12 |
Skriv som tiopotens: