Omkrets, area och volym på Högskoleprovet

Linjära ekvationer Olikheter Procent och promille Talföljder Räta linjens ekvation Enheter och prefix Omkrets, area och volym Medelvärde, median… Tabeller

Andragradsekvationer Bråk och decimaler Räkneregler Funktioner Fyrhörningar Trianglar Sannolikhet Kartor

Ekvationer i bråkformat Potensregler Rötter Potens-/exponentialfunktioner Cirkeln Likformighet Vinklar och parallella linjer Diagram

Lär dig beräkna omkrets, area och volym inför högskoleprovet. Här går vi igenom enhetsomvandling, längd-, area- och volymskala samt de viktigaste formlerna för vanliga geometriska figurer och kroppar.

Sammanfattning Omkrets, area och volym på Högskoleprovet

I slutet av kapitlet för formelsamling om de vanligaste geometriska objekten.
Skalor:

$\text{areaskala} = (\text{längdskala})^2$
$\text{volymskala} = (\text{längdskala})^3$

Omkrets och area

En figurs omkrets är den sammanlagda längden av de linjer och/eller kurvor som avgränsar figuren. Area är ett mått på hur stor figurens yta är. I slutet av kapitlet listar vi formler för omkrets, area och volym för ett antal vanliga geometriska objekt.

Omvandlingstabell för Längd

mil	km	m	dm	cm	mm
1 mil	10	10 000	100 000	1 000 000	10 000 000
	1 km	1 000	10 000	100 000	1 000 000
		1 m	10	100	1 000
			1 dm	10	100
				1 cm	10

Omvandlingstabell för Area

km²	m²	dm²	cm²	mm²
1 km²	10⁶	10⁸	10¹⁰	10¹²
	1 m²	100	10⁴	10⁶
		1 dm²	100	10⁴
			1 cm²	100

Exempel: Omkrets och Area 1

Camp Nou är hemmaarena för fotbollslaget Barcelona FC. Långsidan på Camp Nou är $\text{105 m}$ och arean är $\text{7 140 m^2.}$ Beräkna omkretsen av Barcelonas hemmaplan.

Omkrets av en fotbollsplan

Fotbollsplanen har formen av en rektangel med Arean $=$ Längden $\cdot$ Kortsidan.

$\Rightarrow$ Kortsidan=$\frac{Arean}{Långsidan}=\frac{7140\,m^2}{105\,m} = 68\, m.$

Omkretsen av planen $=$

$= 2($Långsidan $+$ Kortsidan$) =$

$= 2(105 + 68) = 2 \cdot 173 = 346\, m.$

Svar: Omkretsen av fotbollsplanen är $346\,m.$

Exempel: Omkrets och Area 2

Omkretsen av en parallellogram $= 200\, cm.$ En av sidorna $= x\, cm.$ Beräkna den andra sidan.

Parallellogram med sidorna x och y

Vi kallar sidorna i vår parallellogram $= x$ och $y$ och vi söker $y.$

Omkretsen av en parallellogram $= 2(x + y) = 200\, cm.$

Delar vi med $2$ på bägge sidor om likhetstecknet får vi:

$x + y = 100$ vilket ger $y = (100 - x)\, cm.$

Svar: Sidan $= (100 - x)\, cm.$

Exempel: Omkrets och Area 3

$AB = BC = CD = DE = 4$ längdenheter
$AF = FG = GH = 5$ längdenheter

Hur lång är sträckan $\boldsymbol{BH?}$

Sträcka mellan olika punkter

Det finns flera sätt att lösa uppgiften. Enklast är att utgå från en gemensam referenspunkt, exempelvis $A$ och beräkna skillnaden mellan sträckorna $AB$ och $AH:$

$BH = AH-AB=3\cdot5-4=15-4=11$ längdenheter.

Svar: Sträckan $BH=11$ längdenheter.

Volym och Massa

Volym är ett mått på hur mycket något rymmer. Volym används inom fysiken för att bestämma mängden vätska, gas eller solid. Grundenheten för volym är kubikmeter, $m^3$. 1 kubikmeter $= 1 000$ liter, $l.$ Enheten liter används ofta i vardagen, exempelvis $1\, l$ mjölk. $1\, l$ är också lika med $1\,dm^3.$

Deciliter (dl) är en tiondels liter och ofta används i matlagning, exempelvis går det åt $3\, dl$ mjöl till en pannkakssats. Centiliter, cl är en hundradels liter, en burk läsk rymmer exempelvis $33\, cl.$ Milliliter, ml är en tusendels liter och en liten enhet, exempelvis $10\, ml$ hostmedicin. $1\, ml$ är också lika med $1 \,cm^3$.

Omvandlingstabell för Volym

m³	l/dm³	dl	cl	ml/cm³
1 m³	1 000	10⁴	10⁵	10⁶
	1 l/dm³	10	100	1 000
		1 dl	10	100
			1 cl	10

Massa är ett mått på hur mycket materia ett föremål innehåller. Massa används inom fysiken för att beskriva mängden materia i exempelvis fasta ämnen, vätskor och gaser. Grundenheten för massa är kilogram, $kg$. $1$ kilogram $= 1\,000$ gram, $g$. Enheten gram används ofta för mindre massor, exempelvis $500\,g$ mjöl. $1\,g$ är också lika med $1\,000$ milligram, $mg$.

Omvandlingstabell för Massa

ton	kg	hg	g	mg
1 ton	1 000	10 000	1 000 000	1 000 000 000
	1 kg	10	1 000	1 000 000
		1 hg	100	100 000
			1 g	1 000

Exempel: Enheter för volym

Skriv dessa volymer i liter (l):

$2,5\, dm^3 + 5\, dl$
$0,25\, m^3$
$250\, cl + 250\, cm^3$

Svar:

$1\, dm^3 = 1\, l. \Rightarrow 2,5\, dm^3 = 2,5 \cdot 1 l = 2,5\, l.$
$1\, dl = 0,1\, l \Rightarrow 5\, dl = 5 \cdot 0,1\, l = 0,5\, l.$
$\Rightarrow 2,5\, dm^3 + 5\, dl = (2,5 + 0,5)\, l = 3\, l.$
$1\, m^3 = 1 000\, l \Rightarrow 0,25\, m^3 = $
$(0,25 \cdot 1 000)\, l = 250\, l.$
$1\, cl = 0,01\, l$
$\Rightarrow 250\, cl = (250 \cdot 0,01)\, l = 2,5\, l.$
$1\, cm^3 = 0,001\, l.$
$\Rightarrow 250\, cm^3 = (250 \cdot 0,001)\, l =0,25\, l.$
$\Rightarrow 250\, cl + 250\, cm^3 = (2,5 + 0,25)\, l =$
$= 2,75\, l.$

Exempel: Enheter för massa

Skriv dessa massor i kilogram (kg):

$1,2\,ton$
$22\,hg + 800\,g$
$12 \cdot 10^6\,mg$

Svar:

$1\, ton = 1\,000\,kg \Rightarrow 1,2\,ton=1\,200\,kg.$
$10\, hg = 1 \, kg$ och $800\,g = 0,8\,kg$ $\Rightarrow 22\,hg + 800\,g=(2,2+0,8)\,kg=3\,kg$
$10^6\,mg=1\,kg\Rightarrow 12 \cdot 10^6\,mg=12\,kg.$

Exempel: Volymen av en kon

Vad är volymen av en kon med höjden $\boldsymbol{8\,dm}$ och radien $\boldsymbol{3\,dm}?$

Volymen $V$ av en kon $=\frac{\pi r^2 h}{3}$

$V=\frac{\pi 3^2 \cdot 8}{3}=24\pi\,dm^3$

Svar: Volymen $=24\pi\,dm^3$

Skalor

Längdskala

Då vi gör en avbildning av ett föremål på exempelvis ett papper i naturlig storlek är avbildningen lika stor i verkligheten som på pappret. Detta betecknas $1:1.$ I kartor behöver vi ofta göra förminskningar.

En förminskning där $1\, cm$ på kartan motsvarar $1\, m$ i verkligheten betecknar vi $1:100.$
En förminskning där $1\, cm$ på kartan motsvarar $100\, m$ i verkligheten betecknar vi $1:10 000.$

Då en avbildning görs större än föremålet i verkligheten gör vi en förstoring.

En förstoring där $5\,cm$ på ritningen motsvarar $1\,cm$ i verkligheten betecknas $5:1$.
En förstoring där $10\,cm$ på ritningen motsvarar $1\,mm$ i verkligheten betecknas $100:1$.

Exempel: Längdskala

På en karta med skalan $\text{1:5 000 000}$ är avståndet mellan Kalmar och Stockholm ca. $8\, cm.$ Hur långt är det mellan de två städerna i verkligheten?

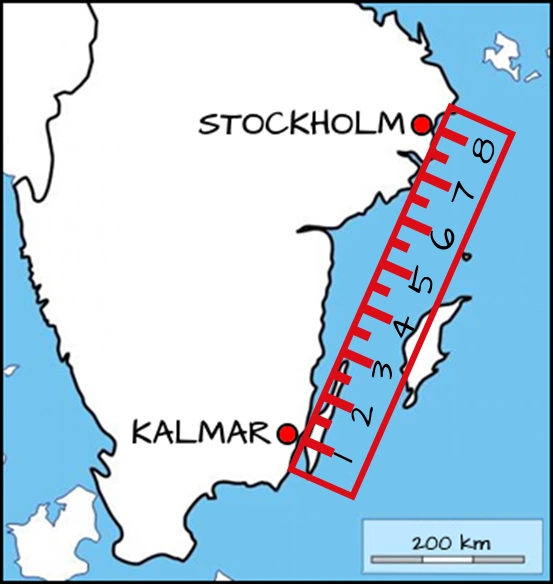
Längdskala i uppgift med karta

Skalan $\text{1:5 000 000}$ innebär att $1\, cm$ på kartan motsvarar $\text{5 000 000}\, cm$ i verkligheten. $\text{5 000 000}\, cm = \text{50 000}\, m = 50\, km.$

$\Rightarrow 8\, cm$ på kartan $= 8 \cdot 50\, km = 400\, km = 40\, mil.$

Svar: Avståndet mellan Kalmar och Stockholm är ca. $40\, mil.$

Areaskala och volymskala

På samma sätt som längdskala beskriver areaskala och volymskala förhållandet mellan en avbildning och verkligheten. Förhållandet mellan längdskala, areaskala och volymskala definieras enligt följande: $$areaskala = (längdskala)^2$$ $$volymskala = (längdskala)^3$$

Om vi studerar enheterna för längd, area och volym finner vi det logiskt med formlerna för omräkning. Grundenheten för längd är meter, för area $meter^2$ och för volym $meter^3.$

Exempel: Längdskala, Areaskala och Volymskala

En kub har volymen $64\,cm^3$ och arean $96\,cm^2$. Bestäm arean och volymen av kuben om alla sidor halveras.

Att halvera sidorna motsvarar i längdskala $1:2.$ Enligt formeln för areaskala och längdskala är areaskalan efter sidohalvering $= (\frac12)^2=\frac14,$ dvs $1:4.$

Arean efter att sidorna halverats $= 96\cdot\frac14=24\; cm^2.$

På samma vis är volymskalan efter sidohalvering $= (\frac12)^3=\frac18$, dvs $1:8$ vilket ger en volym $= 64\cdot\frac18=8\;cm^3$.

Svar: Efter att sidorna halveras är arean $= 24\, cm^2$ och volymen $= 8\, cm^3.$

Formelsamling för Högskoleprovet

Här hittar du de viktigaste formlerna för omkrets, area och volym som är bra att känna till inför högskoleprovet. Formelsamlingen omfattar vanliga geometriska figurer och kroppar som kvadrat, rektangel, triangel, cirkel, kub, rätblock, cylinder, kon och klot.

Objekt	Omkrets och Area
	Kvadrat $Omkrets = 4s$ $Area=s^2$
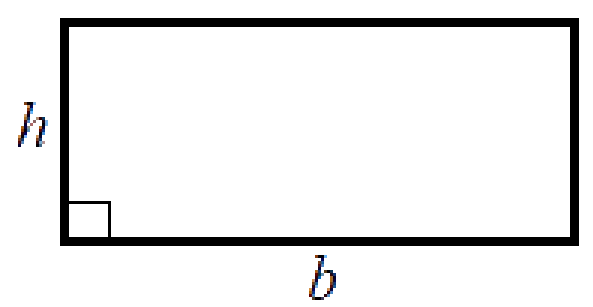	Rektangel $Omkrets = 2(b + h)$ $Area=bh$
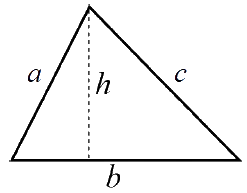	Triangel $Omkrets = a + b + c$ $Area=\frac{bh}2$
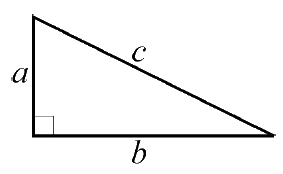	Rätvinklig Triangel Pythagoras sats: $a^2+b^2=c^2$
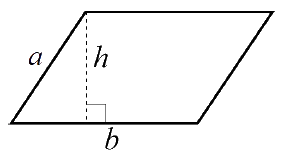	Parallellogram $Omkrets = 2(a + b)$ $Area = bh$
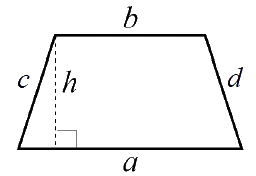	Parallelltrapets $Omkrets = a + b + c + d$ $Area=\frac{h(a+b)}2$
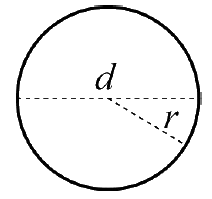	Cirkel $Omkrets = \pi d$ $Area=\pi r^2=\frac{\pi d^2}4$
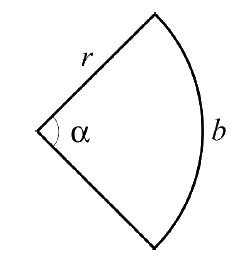	Cirkelsektor $Bågen\:b = \frac{\alpha}{360} \cdot 2 \pi r$ $Area=\frac{\alpha}{360} \cdot \pi r^2=\frac{br}2$
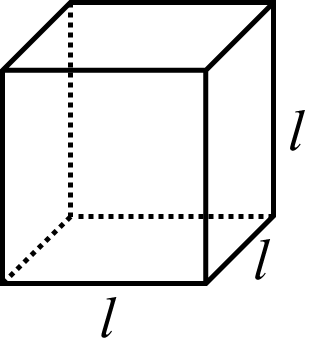	Kub $Volym =l^3$
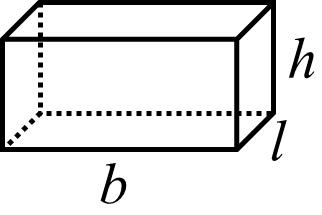	Rätblock $Volym =b \cdot l \cdot h$
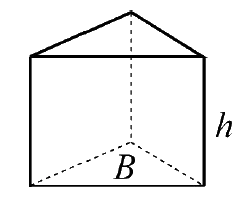	Prisma $Volym =Bh$
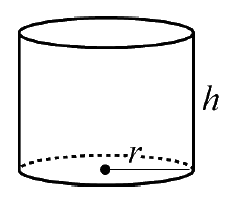	Rak Cirkulär Cylinder $Mantelarea = 2\pi rh$ $Volym=\pi r^2 h$
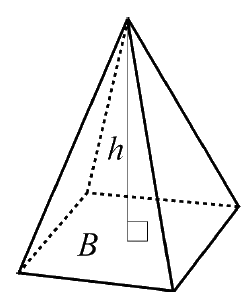	Pyramid $Volym = \frac{B h}3$
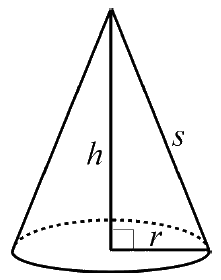	Rak Cirkulär Kon $Mantelarea = \pi r s$ $Volym=\frac{\pi r^2 h}{3}$
	Klot $Area = 4 \pi r^2$ $Volym=\frac{4 \pi r^3}3$
	Skala $\text{Areaskala} = (\text{Längdskala})^2$ $\text{Volymskala} = (\text{Längdskala})^3$