

En andragradsekvation skrivs allmänt på formen: $$ax^2 + bx + c$$ och en motsvarande andragradsfunktion (se avsnittet om Potensfunktioner): $$f(x) = ax^2 + bx + c$$ Enkla andragradsekvationer är sådana ekvationer som endera saknar $x$-term ($b = 0$), t.ex. $x^2 - 25 = 0$ eller konstant ($c = 0$), t.ex. $x^2 - 4x = 0$. Dessa ekvationer kan vi lösa genom faktorisering eller genom att flytta över konstanttermen till högerledet och beräkna roten ur respektive led.
Bestäm rötterna till ekvationen $\boldsymbol{x^2 - 25 = 0}$
Vi flyttar över konstanten till högerledet och kan lösa ekvationen direkt genom att dra roten ur bägge led:$x^2=25\Rightarrow x =\pm \sqrt{25}\Rightarrow x = \pm 5$
Svar: $x_1 = 5, x_2 = -5$. Motsvarande funktion $f(x) = x^2 - 25$ enligt nedan.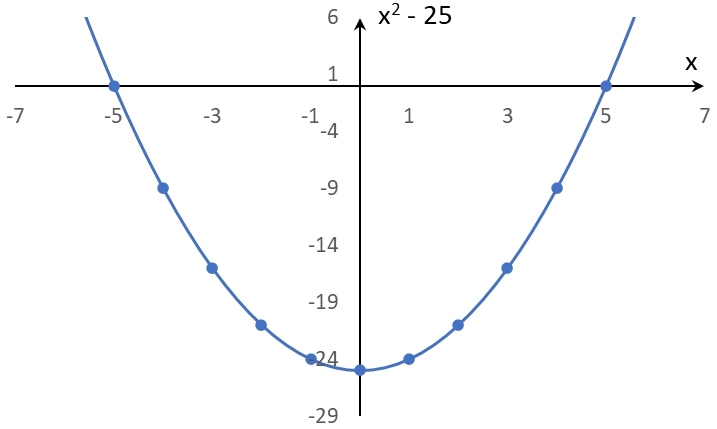
Bestäm rötterna till ekvationen $\boldsymbol{x^2 - 4x = 0}$
$x^2 - 4x = x(x - 4) = 0$
Då vi faktoriserat talet enligt ovan är det enkelt att bestämma de två rötterna. Den ena roten får vi om vi sätter det som står utanför parentesen i vänsterledet (dvs $x$) lika med högerledet (dvs $0$). På samma sätt beräknar vi den andra roten om vi sätter det som står innanför parentesen (dvs $x - 4$) till högerledet. Den här metoden kallas nollproduktmetoden.
Svar: $x_1 = 0, x_2 = 4$. Motsvarande funktion $f(x) = x^2 - 4x$ enligt nedan.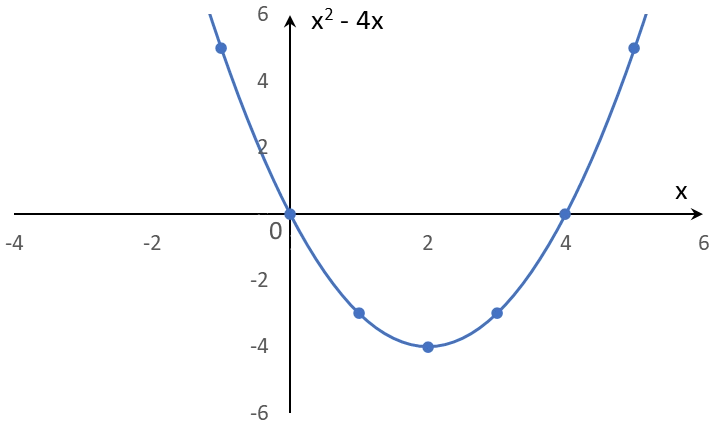
Då vi inte har tillgång till dator och ska beräkna kvadraten av ett tal kan vi utnyttja att kvadraten av ett tal kan skrivas $x^2=(x+d)(x-d)+d^2$ eller $x^2=(x-d)(x+d)+d^2$ där $x$ är talet i kvadrat och $d$ är differensen.
Exempel: $63^2=$
$=(63-3)(63+3)+3^2=$
$=60\cdot66+9=$
$=60(60+6)+9=$
$=3600+360+9=$
$=3969$
Vad är $\boldsymbol{74^2?}$
$74^2=(74-4)(74+4)+4^2=$
$=70\cdot78 + 16=$
$=70(70+8)+16=$
$=4900+ 560+16=5476$
Då vi ska lösa ekvationer på formen $ax^2 + bx + c$ och då vi har värden på både x-termen (dvs $b \neq 0$) och konstanten (dvs $c \neq 0$) kan vi endera göra kvadratkomplettering eller utnyttja pq-formeln:
$$x=-\frac{p}{2}\pm\sqrt{\left (\frac{p}{2} \right )^{2}-q}$$ $$p=\frac ba \text{ och } q=\frac ca$$Bestäm lösningen till ekvationen $\boldsymbol{x^{2}+8x+7=0}$
Vi utnyttjar pq-formeln. I det här fallet är $p = 8$ och $q = 7$. pq-formeln ger:
$x=-\frac{8}{2}\pm\sqrt{\left (\frac{8}{2} \right )^{2}-7}$
$x=-\frac{8}{2}\pm\sqrt{16-7}$
$x=-4\pm\sqrt{9}$
$x=-4\pm 3$.
Svar: $x_1 = -1, x_2 = -7$. Motsvarande funktion $f(x) = x^{2}+8x+7$ enligt nedan.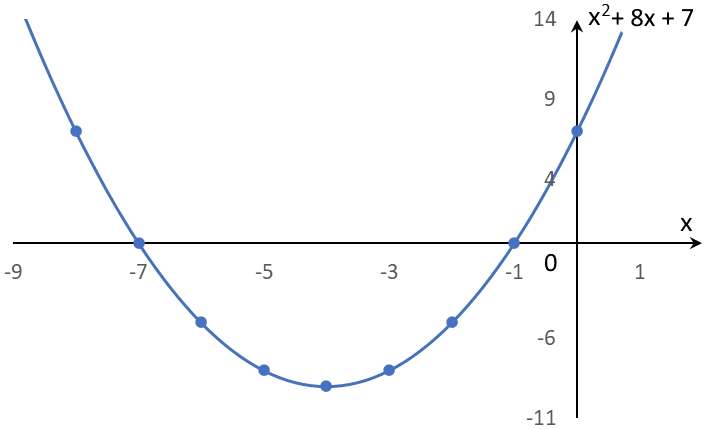
Beräkna $\boldsymbol{(x + 2) \cdot (x - 2)}$
Enligt konjugatregeln:
$(x + 2) \cdot (x - 2) = x^2 - 2^2 = x^2 - 4$
Svar: $x^2 - 4$Bestäm $\boldsymbol{(x + 2)^2}$
Enligt första kvadreringsregeln:
$(x + 2)^2 = x^2 + 2^2 + 2 \cdot x \cdot 2 = x^2 + 4 + 4x$
Svar: $x^2 + 4 + 4x$Bestäm $\boldsymbol{(x - 2)^2}$
Enligt andra kvadreringsregeln:
$(x - 2)^2 = x^2 + 2^2 - 2 \cdot x \cdot 2 = x^2 + 4 - 4x$
Svar: $x^2 + 4 - 4x$I vissa uppgifter gör ett variabelbyte att vi förenklar ekvationen och kan lösa den snabbare. Variabelbyte är mycket användbart för mer komplicerade uppgifter än de som ska lösas på högskoleprovet, men kan ibland passa mycket bra även för uppgifterna på högskoleprovet. Variabelbyte går ut på att ersätta vissa termer i ekvationen för att förenkla ekvationen, ofta genom utnyttjande av konjugatregeln eller kvadreringsreglerna.
Kvadratkomplettering går också ut på att använda kvadreringsreglerna. Vi "möblerar om" ekvationen så att den passar den första eller den andra kvadreringsregeln.
Vissa andragradsekvationer kan faktoriseras genom den sk. inspektionsmetoden.
$$x^2+b\,x+c=(x+p)(x+q)$$ $$p+q=b\text{ och } p\cdot q = c$$Vilket ger $x_1=-p$ och $x_2=-q$. I det fall vi enkelt kan kan hitta $p$ och $q$ är detta ett snabbare sätt att lösa andragradsekvationer än exempelvis pq-formeln.
Bestäm $\boldsymbol{x}$ för ekvationen $\boldsymbol{(x+1)^2-4=0}$
Vi ersätter $(x + 1)$ med $u$ och skriver om vår ekvation:
$u^2-4=0 \Rightarrow u^2=4 \Rightarrow u = \pm 2$
Nu ersätter vi tillbaka $u$ med $(x + 1)$:
$x + 1 = \pm 2 \Rightarrow x = -1 \pm 2$
Svar: $x=1$ eller $x=-3$Vad är rötterna till ekvationen $\boldsymbol{{x^2+4x-5=0}?}$
Vi börjar med att flytta konstanttermen till högerledet:
$x^2+4x=5$
Strategin är att faktorisera vänsterledet med hjälp av den första kvadreringsregeln. Om x-termen vore negativ hade vi utnyttjat den andra kvadreringsregeln. Första kvadreringsregeln skrivs $x^2+2bx+b^2=(x+b)^2$. För att få vårt vänsterled på den här formen behöver vi alltså lägga till en konstantterm $b^2$, samtidigt som $2bx$ ska vara lika med x-termen i vårt vänsterled, vilket ger $2bx = 4x \Rightarrow b = 2$.
Vi lägger till $b^2 = 2^2$ i både vänsterledet och högerledet i vår ekvation, vilket ger:
$x^2+4x + 2^2 = 5 + 2^2 \Rightarrow (x+2)^2=9$
$x + 2 = \pm 3 \Rightarrow x = -2 \pm 3$.
Svar: $x=1$ eller $x=-5$Vad är alla lösningar till ekvationen $\boldsymbol{x^2 + x - 12 = 0?}$
Vi söker $p$ och $q$ så att vi kan faktorisera $x^2 + x - 12 = (x+p)(x-q)$
Enligt inspektionsmetoden ska $p$ och $q$ väljas så att $p+q=1$ och $p \cdot q = -12$
Prövning ger oss att $p=4$ och $q=-3$:
$x^2 + x - 12 = 0 \Rightarrow (x+4)(x-3)=0$
$x_1 = -4$ och $x_2=3$
Svar: $x = -4$ eller $x=3$En ekvation med ett högre gradtal, exempelvis $x^2, x^3$, osv., har normalt lika många lösningar (rötter) som gradtalet, fast flera av lösningarna kan vara samma. Dvs, en ekvation med $x^2$-term har normalt två lösningar, en ekvation med $x^3$-term har normalt tre lösningar, osv.
Att en andragradsekvation har samma lösning brukar kallas dubbelrötter, exempelvis ekvationen $x^2 - 4x + 4 = 0$, vilket ger $x_1 = 2$ och $x_2 = 2$.
Som exemplet nedan visar så har inte alla ekvationer en lösning.
Bestäm lösningen till ekvationen $\boldsymbol{2y^2 + 50 = 0}.$
Vi börjar med att dividera vänsterledet och högerledet med $2$ för att få koefficienten framför $y = 1$:
$\frac{2y^2 + 50}2 = \frac02$
$y^2 + 25 = 0$. Därefter flyttar vi konstanten $25$ till högerledet:
$y^2 = -25\Rightarrow y=\pm \sqrt{-25}$
Vi ser då att vi får ett negativt tal under rottecknet. Det innebär att ekvationen inte har några reella rötter. Om vi ritar kurvan till ekvationen $2y^2 + 50$ så ser vi att den aldrig skär x-axeln och därmed saknar nollställen.
Svar: Ekvationen saknar lösning (för reella tal). Motsvarande funktion till $2y^2 + 50$ enligt nedan.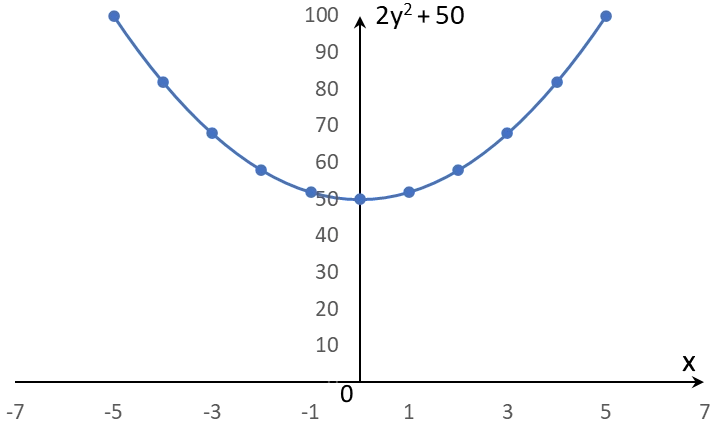
Som vi tidigare beskrivit har andragradsekvationer normalt två lösningar, men vissa andragradsekvationer har bara en lösning eller saknar lösning helt. Studerar vi pq-formeln så kan vi avgöra hur många lösningar en andragradsekvation har. Det som står innanför för rottecknet, dvs $\left (\frac{p}{2} \right )^{2}-q$, kallas diskriminanten. Utgående från värdet på diskriminanten ger det oss tre olika möjligheter:
Grafiskt innebär det här:
För vilket värde på konstanten $\boldsymbol{a}$ har ekvationen $\boldsymbol{x^2 = 4a - 8}$ exakt en lösning?
Det är lätt att bli lurad av uppgiften och tolka att termen $4a$ hör till x-termen, men det stämmer inte. Istället är hela termen $4a - 8$ en konstant och x-term saknas i ekvationen. Vi provar därför att sätta $a$ lika med de olika värden vi finner bland våra svarsalternativ:
Svaret är därför B, dvs för $a = 2$.
Svar: Alternativ B.För vilka värden på konstanten $\boldsymbol{k}$ har ekvationen $\boldsymbol{x^2 + kx + 25}$ exakt en lösning?
$p=\frac ba = \frac{k}{1}=k$ och $q=\frac {25}{1}=25$
Diskriminanten $=\left (\frac{k}{2} \right )^{2}-25=\frac{k^2}{4}-25$
Vi vill beräkna $k$ så att diskriminanten $= 0,$ dvs.
$\frac{k^2}{4}-25=0$
$k^2=100 \Rightarrow k = \pm \sqrt{100}=\pm 10$
Svar: $k = \pm 10$.