



Vad är $\boldsymbol{a?}$

Diagonalen i en kvadrat delar in kvadraten i två rätvinkliga och likbenta trianglar med kateterna lika med kvadratens sida. I rätvinkliga trianglar kan vi använda Pythagoras sats:
$a = \sqrt{10^2+10^2}=\sqrt{2 \cdot 10^2}=10 \sqrt{2}$
Svar: $a = 10 \sqrt{2}$
Diagonalen i en kvadrat är alltid lika med sidan multiplicerat med roten ur två.
I kvadraten $ABCD$ med sidan $x$ är $M$ mittpunkten på sidan $AB,$ $N$ är mittpunkt på sidan $CD$ och $O$ är mittpunkt på sidan $NC.$ Vad är arean $\boldsymbol{AMOD?}$

$AMOD$ kan vi dela upp i en rektangel med sidorna $\frac{x}{2}$ och $x$ och en triangel med basen $\frac{x}{4}$ och höjden $x:$
Arean av rektangeln $= x \cdot \frac{x}{2} = \frac{x^2}{2}$
Arean av triangeln $= \frac{x \cdot \frac{x}{4}}{2}=\frac{x^2}{8}$
Arean av $AMOD = \frac{x^2}{2} + \frac{x^2}{8} = \frac{4x^2+x^2}{8}=\frac{5x^2}{8}$
Svar: Arean $AMOD = \frac{5x^2}{8}$
Två likbenta och rätvinkliga trianglar med samma bas och höjd med längden $s$ sammanfogas enligt figuren nedan. Arean av den sammanfogade figuren är $36\,cm^2$. Hur lång är längden $\boldsymbol{d}$ i den sammanfogade figuren?
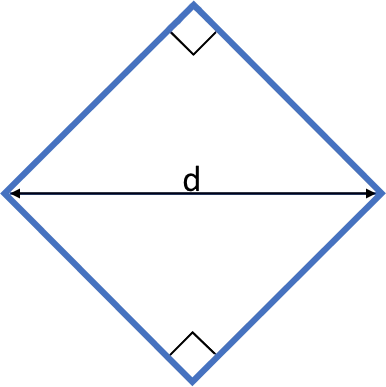
Vi vet att diagonalen $d$ av alla kvadrater kan beräknas som $d=\sqrt{2}\cdot s$. Sidan $s$ beräknar vi som $\sqrt{arean}=\sqrt{36}=6\,cm.$ Vilket ger oss $d=6\sqrt{2}\,cm.$
Svar: $d=6\sqrt{2}\,cm.$
Kvadraten $K_1$ är inskriven i en cirkel med mittpunkten $M$. En annan kvadrat $K_2$ omskriver samma cirkel. De två kvadraternas respektive sida tangerar cirkeln enligt figuren nedan.
Kvantitet I: Arean av $K_2$
Kvantitet II: $2\cdot$ Arean av $K_1$

För att beräkna $s_1$ använder vi pythagoras sats: $s_1^2+s_1^2=(2r)^2$
$2s_1^2=4r^2$
$s_1^2=2r^2 \Rightarrow s_1=\sqrt{2}r$
Kvantitet I $=$ Area $K_2=s_2^2=(2r)^2=4r^2$
Kvantitet II $=2s_1^2=2(\sqrt{2}r)^2=4r^2$
Kvantitet I = II.

Svar: Kvantitet I = II
Vad är a?

På samma sätt som i en kvadrat, så delar diagonalen i rektangeln upp den i två rätvinkliga trianglar. Däremot är inte trianglarna likbenta som då vi delar upp kvadraten med en diagonal. Vi använder Pythagoras sats för att beräkna $a:$
$a = \sqrt{5^2+10^2}=\sqrt{125}$
Svar: $a = \sqrt{125}$

I en parallellogram är motstående sidor parallella och lika långa. Vinklarna i en parallellogram kan vara räta, men behöver inte vara det. Om en vinkel i en parallellogram är rät, så är de övriga vinklarna också räta. Motstående vinklar i parallellogrammen är lika stora, dvs vinkeln $A =$ vinkeln $D$ och vinkeln $B =$ vinkeln $C.$
Om två närliggande sidor i en parallellogram är lika stora, så är parallellogrammen liksidig. I en parallellogram halverar diagonalerna varandra. Diagonalen delar en parallellogram i två kongruenta trianglar, dvs motsvarande sidor är lika långa och motsvarande vinklar är lika långa.
En romb är en parallellogram där fyrhörningens alla sidor har samma längd.
$$Omkrets = 2(a+b)$$ $$Area=bh$$ $$Vinkelsumma = A+B+C+D=360^o$$
$ABCD$ är en parallellogram. Vad är y?

Vinkelsumman i en parallellogram är $360^o$ och motstående vinklar är lika stora vilket ger oss:
$2(4y + 5y) = 360^o$
$18y = 360^o$
$y = \frac{360^o}{18} = 20^o$
Svar: $y = 20^o$
Beräkna omkretsen av parallellogrammen om längden på den horisontella sidan är $\boldsymbol{12\, cm.}$
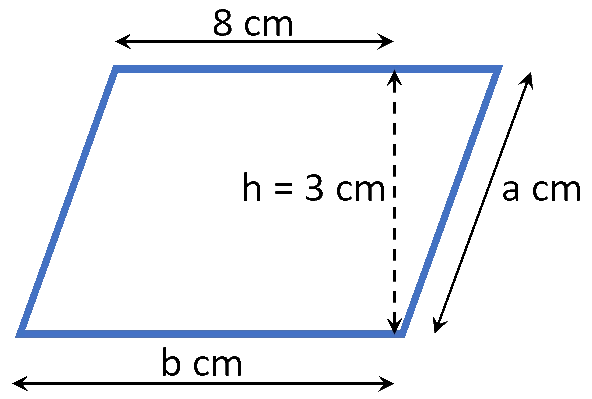
Omkretsen av en parallellogram är $2(a + b).$ Enligt texten är basen, $b = 12\, cm.$ Vi använder pythagoras sats för att beräkna sidan $a,$ där $a$ utgör hypotenusan av triangeln med basen $(12 - 8) = 4\, cm$ och höjden $3\, cm:$
$a^2=4^2+3^2 \Rightarrow b = \sqrt{16 + 9} = \sqrt{25}=5$
Omkretsen $= 2(a + b) = 2(5 + 12) = 34\, cm.$
Svar: Omkretsen $= 34\, cm.$
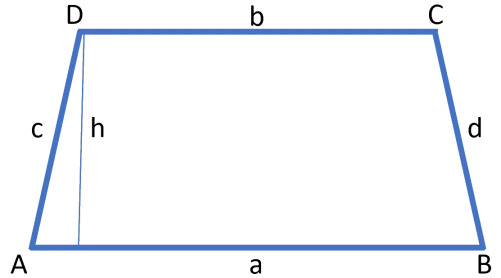
Ett parallelltrapets är en fyrhörning där två sidor är parallella. I ett likbent trapets är vinklarna vid basen lika stora $($vinkeln $A =$ vinkeln $B),$ de icke-parallella sidorna lika stora $($sidan $c =$ sidan $d)$ och motstående vinklar är supplementvinklar $($vinkeln $A +$ vinkeln $D = 180^o$ och vinkeln $B +$ vinkeln $C = 180^o).$
$$Omkrets = a+b+c+d$$ $$Area=\frac{h(a+b)}{2}$$ $$Vinkelsumma = A+B+C+D=360^o$$
I det likbenta parallelltrapetsen är vinkeln $XYZ = 3x + 19$ och vinkeln $WXY = x + 1.$ Beräkna $\boldsymbol{x.}$
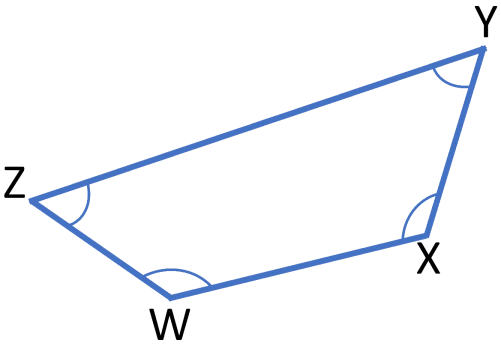
Vi vet att i ett likbent parallelltrapets är motstående vinklar supplementvinklar, dvs:
$XYZ + WXY = 180^o$
$(3x + 19) + (x + 1) = 180^o$
$4x + 20 = 180^o$
$x = \frac{180-20}{4} = 40^o$
Svar: $x = 40^o$