

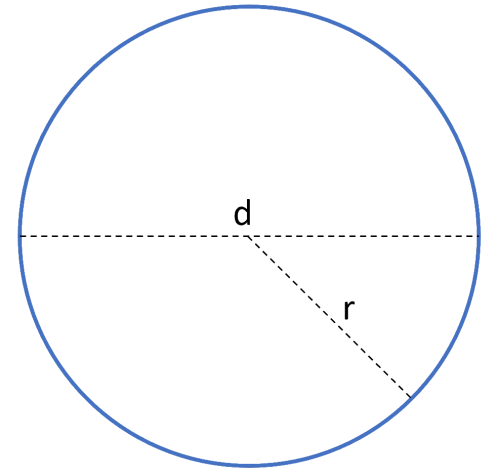
Cirkeln är en av de grundläggande geometriska formerna. Cirkelns radie är avståndet från mittpunkten till cirkelns periferin, markerat r i figuren. Diametern är avståndet från perierin genom mittpunkten till periferin på motstående sida, markerat d i figuren. $$Omkrets= \pi d = 2\pi r$$ $$Area= \pi r^2=\frac{\pi d^2}{4}$$
En pizza bakas på en kvadratisk plåt med arean $400\, cm^2$. Pizzabagaren försöker att minimera degspillet genom att utnyttja så mycket av plåten som möjligt. Bestäm arean av den del av plåten (det svarta området i figuren) som pizzan inte täcker.
Plåtens area - Pizzans area.
Arean av plåten = $sidan^2$
$\Rightarrow sidan =\sqrt{400}=20\: cm$
Vi antar att pizzan är cirkulär och då den tangerar plåtens sida är pizzans diameter $=$ plåtens sida $= 20\, cm.$
Pizzans area $= \frac{\pi d^2}{4}=\frac{\pi \cdot 20^2}{4}=100\pi$
Arean av plåten som pizzan inte täcker $=$
$= 400\, cm^2 - 100 \pi \approx 86\, cm^2$
Svar: Arean av plåten som pizzan inte täcker $\approx 86\, cm^2$Inskrivna geometriska objekt (exemplet med pizzan) har tillämpning inte enbart genom att minimera degspill för pizzabagare. Andra exempel är formgjutning inom industrin och lastoptimering.
En cirkel är inskriven i ett koordinatsystem. Sträckan $AB$ är cirkelns diameter där punkten $A$ har koordinaterna $(-5, -1)$ och punkten $B (3, 5).$ Bestäm cirkelns area.
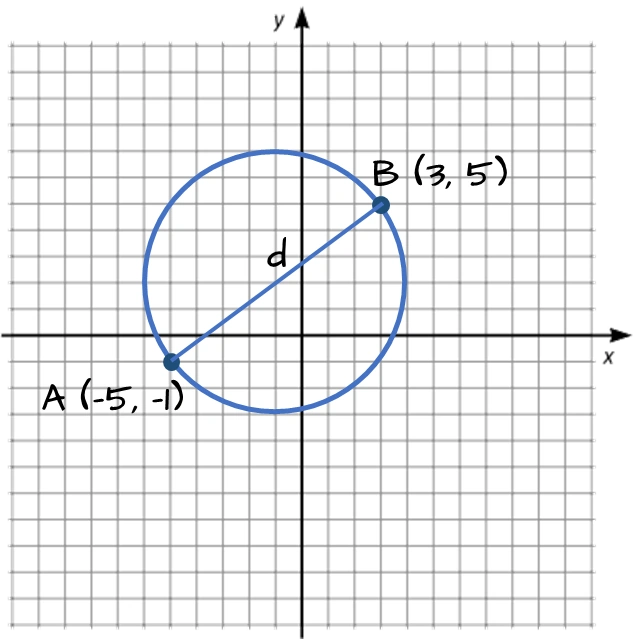
I kapitlet om räta linjens ekvation lärde vi oss att vi kan använda avståndsformeln för att beräkna avståndet mellan två punkter.
Avståndet mellan punkten $A (x_1, y_1)$ och punkten $B (x_2, y_2)$ är lika med cirkelns diameter $d:$
$d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}$. Med våra koordinater insatt får vi:
$\sqrt{(3--5)^{2}+(5--1)^{2}}=$
$=\sqrt{64+36}=\sqrt{100}=10$
Cirkelns area $= \frac{\pi d^2}{4}=\frac{\pi 10^2}{4}=25 \pi$
Svar: Cirkeln area $= 25\pi$ areaenheterEtt cykelhjuls diameter är $64\, cm.$ Hur många varv rullar hjulet på en sträcka av en kilometer?
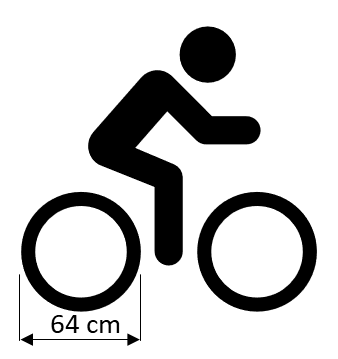
Låt oss kalla diametern på hjulet $= d.$ På ett varv rullar hjulet $\pi \cdot d=\pi \cdot 0,64 = 0,64\pi$ varv.
På $1\, km = 1 000\, m$ rullar hjulet $\frac{1000}{0,64\pi}\approx 500$ varv.
Svar: Hjulet rullar cirka $500$ varv på $1\, km.$Cirkeln B:s radie är $\frac34$ gånger mindre än cirkeln A:s. Vad är arean $\boldsymbol{A?}$

A:s radie är $(3 + x)$ längdenheter och B:s radie är $(2 + x)$ längdenheter. Enligt texten är B:s radie $\frac34$ gånger mindre än A:s, vilket vi kan uttrycka:
$\frac34(3+x)=2+x$
$\frac94 + \frac{3x}{4}=2+x$
$\frac{x}{4}=\frac14 \Rightarrow x = $ 1 längdenheter.
Arean A = $\pi(3+1)^2=16\pi$ areaenheter.
Svar: Arean $A$ är $16\pi$ areaenheter.Vad är arean av den största kvadrat som ryms i en cirkel med radien $\boldsymbol{r?}$

Kvadratens diagonal är $2r$ och vi kallar kvadraten sida $s.$
Pythagoras ger: $(2r)^2 = s^2 + s^2$
$4r^2=2s^2 \Rightarrow 2r^2=s^2 \Rightarrow s=\sqrt{2}r$
Arean av kvadraten är $s^2=(\sqrt 2 r)^2 = 2r^2$
Svar: Arean $=2r^2$
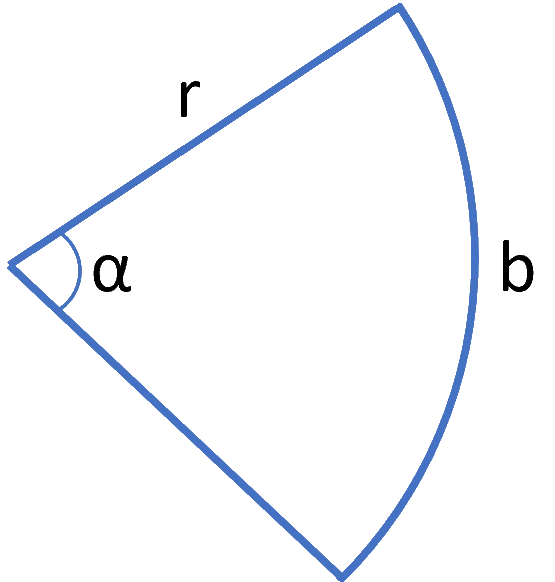
En sammanhängande del av cirkeln kallas cirkelsektor. Storleken på cirkelsektorn i förhållande till tillhörande cirkel bestäms av medelpunktsvinkeln $\alpha$.
En cirkelsektor har radien $1\, cm$ och medelpunktsvinkeln $60$ grader. Beräkna dess omkrets och area.
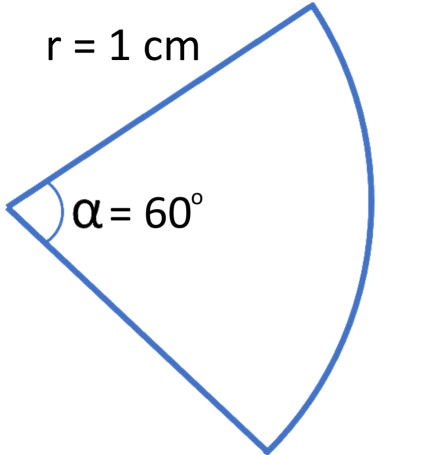
Omkretsen $= 2 \cdot$ radien $+$ längden på bågen $=$
$= 2r + b$
$b = \frac{\alpha}{360}\cdot 2 \pi r =\frac{60}{360}\cdot 2 \pi \cdot 1=$
$=\frac{1}{60}\cdot 2 \pi \approx 1,0\, cm.$
Vi kan nu beräkna omkretsen $=$
$= 2 \cdot 1 + 1,0 = 3,0\, cm.$
Arean $= \frac{br}{2} = \frac{1 \cdot 1}{2} \approx 0,5\, cm^2$
Svar: Cirkelsektorns omkrets $= 3\, cm$ och arean $= 0,5\, cm^2.$Hur långt rör sig gungan mellan sina två vändlägen?

Sträckan som gungan rör sig mellan sina två vändlägen har formen av en cirkelsektor med medelpunktsvinkeln $2 \cdot 67,5^o = 135^o$. Längden på gungans linor kan vi likställa med radien på cirkeln. Därmed kan vi beräkna sträckan $s:$
$s = \frac{135^o}{360^o}\cdot 2 \pi \cdot 2 = \frac38 \cdot 4 \pi=\frac{3 \pi}{2} m$
Svar: Gungan rör sig $\frac{3 \pi}{2} m.$ Arean av plåten som pizzan inte täcker $=$
Arean av plåten som pizzan inte täcker $=$