








De diagram som vanligen förekommer på högskoleprovet är cirkeldiagram och ringdiagram (även kallat munkdiagram), histogram, linjediagram och kurvdiagram, punktdiagram (även kallat sambandsdiagram eller spridningsdiagram), bubbeldiagram, radardiagram, stapeldiagram och stolpdiagram, ytdiagram (även kallat areadiagram), flödesdiagram och kombinationsdiagram.
Diagram utgår från tabeller (som beskrivs i nästa avsnitt), men är ett bättre sätt att visualisera data för att snabbare dra slutsatser om trender, proportionalitet, andelar, etc. Du behöver kunna tolka diagram och förstå innebörden, läsa av värden och dra slutsatser utifrån detta samt besvara frågor relaterade till diagrammets underliggande data.
På DTK på Högskoleprovet beskriver vi hur du förbereder dig på bästa sätt till Högskoleprovet genom att förstå diagram, tabeller och kartor.
Cirkeldiagram och ringdiagram (munkdiagram) använder vi för att identifiera inbördes förhållanden i en fördelning som andel av totalen, exempelvis utfallet av ett riksdagsval med röstandelar på olika politiska partier. Totalen representeras av hela cirkeln. Om uttryckt i procent är hela cirkeln lika med 100% och summan av varje cirkelsektor (tårtbit) är totalt lika med 100%.
Ett bra sätt att läsa av ett cirkeldiagram är att tänka på diagrammet som en klocka där timmarna i klockan delar upp diagrammet i 12 delar. Vi börjar högst upp i mitten (klockan 12) och går medsols runt diagrammet. Varje andel är $\frac{1}{12}$. Klockan 3 är andelen $\frac{3}{12}=\frac14$, klockan 5 är andelen $\frac{5}{12}$, och så vidare. Se figuren nedan.

Ringdiagram (även kallat munkdiagram, från engelskans donut chart) är en variant av cirkeldiagrammet med samma användningsområde. Ringdiagrammet har ett hål i centrum och visar de ingående andelarna som cirkelbågar istället för cirkelsektorer. På Interaktiva övningsprov kan du se ett exempel på ringdiagram där vi visualiserar status av övningsprovet med ett ringdiagram.
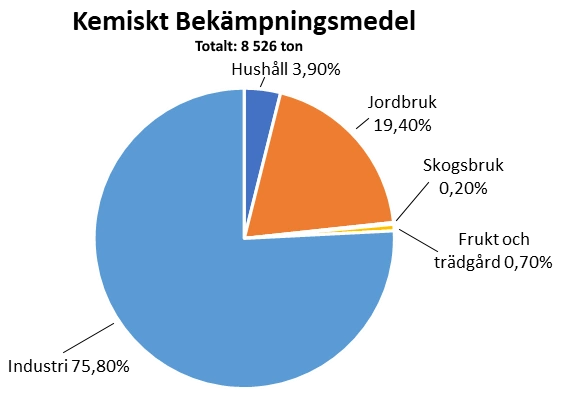
Hur många fler ton kemiskt bekämpningsmedel såldes till sektorn Jordbruk än till sektorn Frukt och trädgård?
Vi läser av cirkeldiagrammet och noterar att sektorn Jordbruk står för 19,4% och sektorn Frukt och trädgård för 0,7%. Skillnaden mellan dessa sektorer är 19,4% - 0,7% = 18,7%.
Över diagrammet läser vi att totalen är 8526 ton. Skillnaden mellan sektorerna i ton är således $8526\cdot 0,187 \approx 8000 \cdot 0,2 = 1600$ ton.
Svar: 1600 ton.
Ett histogram delar in datamängden i olika intervall, kallat klasser, där klasserna är lika stora längs den horisontella axeln och antalet förekomster, kallat frekvens, längs den vertikala axeln. Histogram används för att gruppera en datamängd där utfallet kan variera stort, exempelvis fördelning av ålder, längd, vikt, tid, etc.
40 personer deltar i ett prov med 6 frågor. Vad är medianpoängen?
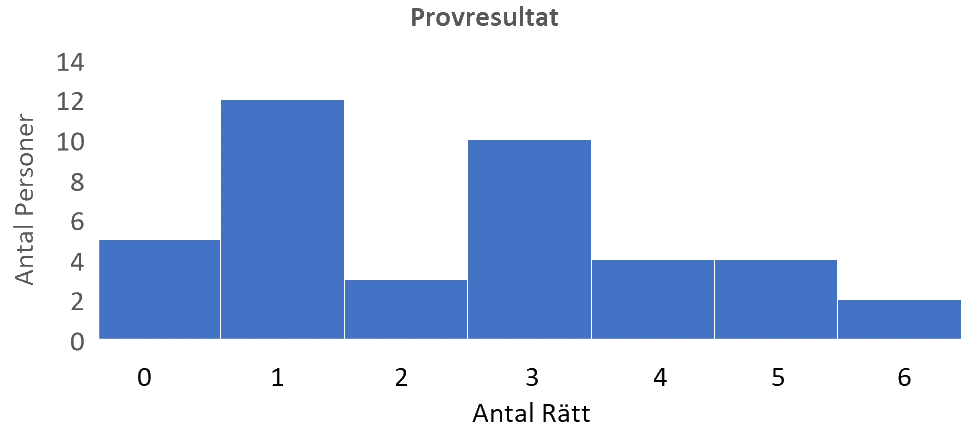
Vi söker medianen för ett prov som är skrivet av totalt 40 personer. I histogrammet är poängen redan sorterade efter storleksordning, vilket är en förutsättning för att beräkna medianen. Eftersom provet skrivits av ett jämnt antal personer är medianen lika med medelvärdet av resultatet av den 20:e och den 21:a personen. Vi läser av diagrammet och konstaterar:
Medianen är således =$\frac{2+3}{2}=2,5$ p.
Svar: Medianen är 2,5 p.Linjediagrammet använder vi ofta för att visualisera data som förändras över tiden. Vi skapar linjediagrammet genom att plotta flera värden i diagrammet och sedan förbinda dessa med en linje. Linjediagrammet är kanske det vanligaste förekommande diagrammet och det återfinns ofta i uppgifter i högskoleprovet.
Kurvdiagrammet fungerar på samma sätt som linjediagrammet. Skillnaden är att de olika mätvärdena binds samman med en kurva istället för en rät linje.
Studera det högsta och det lägsta vattenstånd som uppmättes i Mälaren under 1996. Hur stor var skillnaden?
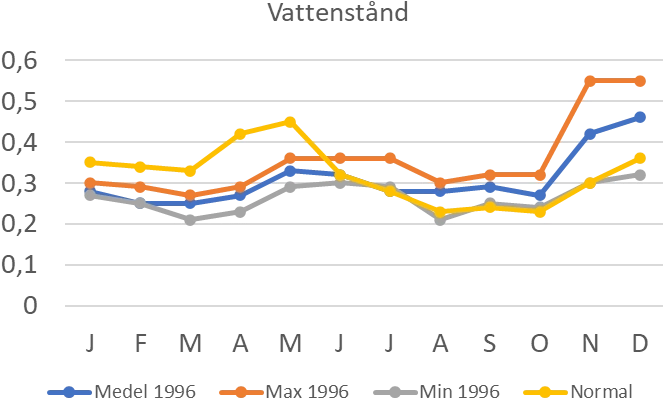
Det högsta vattenståndet som uppmättes i Mälaren 1996 var ungefär 0,55 m.ö.h. och det lägsta vattenståndet ungefär 0,21 m.ö.h. Skillnaden mellan det högsta och det lägsta vattenståndet var $0,55-0,21=0,34$ meter.
Svar: 0,34 meterEtt punktdiagram visar alltid relationen mellan två variabler längs den vertikala axeln och den horisontella axeln och koordinaterna för den punkt (kallad datapunkt) där variablerna möts markeras med en punkt. Bubbeldiagram liknar punktdiagrammet och här markeras datapunkten med en bubbla. Storleken på bubblan avgörs av en tredje dimension. Genom att animera bubbeldiagrammet kan en fjärde dimension (ofta tid) införas.
På en marknad finns fem bolag: Alpha, Beta, Gamma, Delta och Epsilon, med finansiell nyckeldatata enligt diagrammet nedan. Hur mycket större är Epsilon än Alpha vad gäller omsättning, antal produkter och marknadsandel?
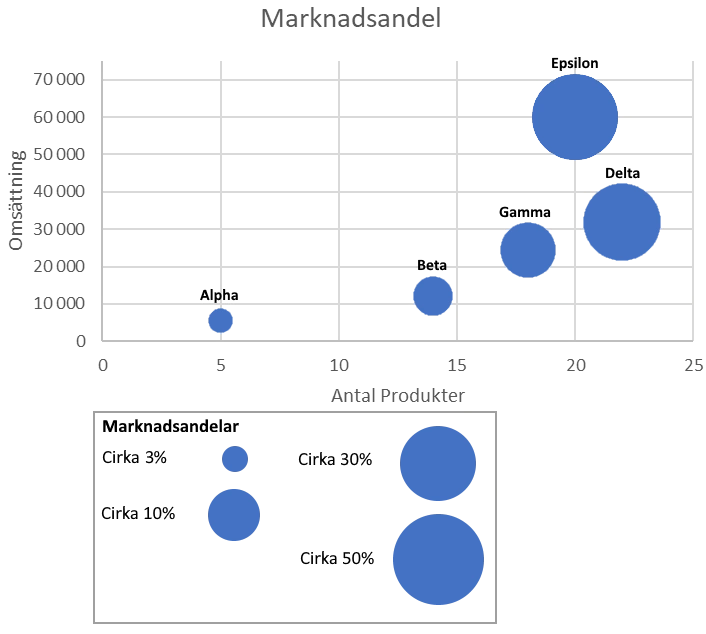
Diagrammet visar omsättning på den vertikala axeln som funktion av antal produkter på den horisontella axeln. Storleken på bubblorna anger marknadsandel i procent med förklaring under diagrammet. Vi börjar med att analysera bolaget Epsilon:
Notera att då vi läser av värden på axlarna så utgår vi alltid från mittpunkten (centrum) av bubblan. Nu analyserar vi Alpha på samma sätt:
Skillnaden mellan de två bolagen är således:
Radardiagram (inland kallat spindelnätsdiagram) är vanliga för att visualisera information som utgår från samma nollpunkt, men där kategorierna inte nödvändigtvis är direkt jämförbara.
Hur stor var den redovisade solinstrålningen vid den vanligast förekommande vindriktningen?
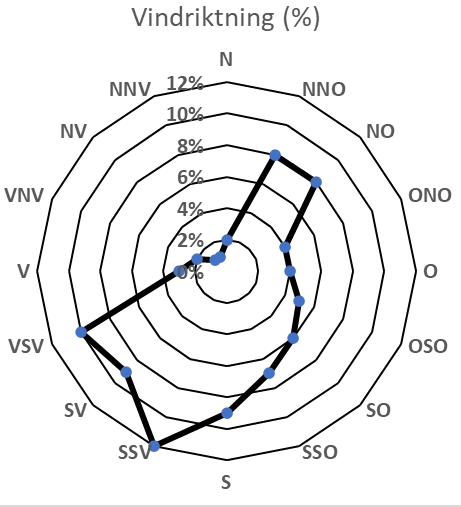
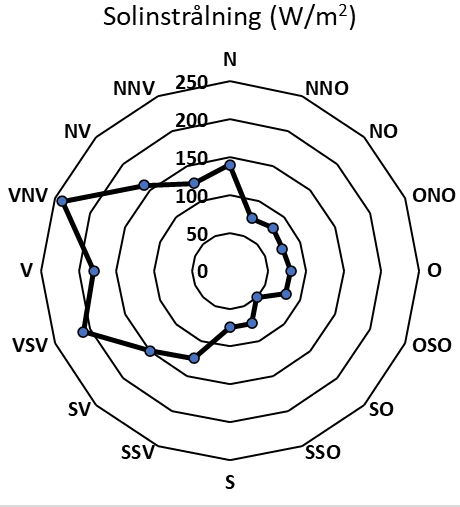
Vi får två olika diagram som underlag för uppgiften och använder det första diagrammet för att bestämma den vanligaste vindriktningen och sedan det andra för att bestämma solinstrålningen.
Det första diagrammet ger oss informationen att den vanligaste vindriktningen är Sydsydväst (SSV) och 12%. Vi undersöker därefter det andra diagrammet och noterar att solinstrålningen för vindriktningen SSV är 125 W/m2.
Svar: Solinstrålningen är 125 W/m2 (för vindriktningen Sydsydväst).Stapeldiagram och stolpdiagram förekommer ofta i uppgifter på högskoleprovet. Ett stolpdiagram har smalare bas än stapeldiagrammet och används ofta med numerisk data (siffror) längs den horisontella axeln istället för diskret data (exempelvis ja/nej/vet ej). Stapeldiagram och stolpdiagram finns både som stående variant och som liggande. Den enda skillnaden är om kategoriaxeln respektive värdeaxeln finns på den horisontella axeln eller vice-versa. Ett stafflat stapeldiagram liknar ytdiagrammet på det sätt att varje mätserie staplas ovanpå varandra vilket möjliggör att identifiera seriernas andel av totalen.
Hur många var de kvinnor som dog av sjukdomar i cirkulationsorganen jämfört med de kvinnor som dog av sjukdomar i matsmältningsorganen?
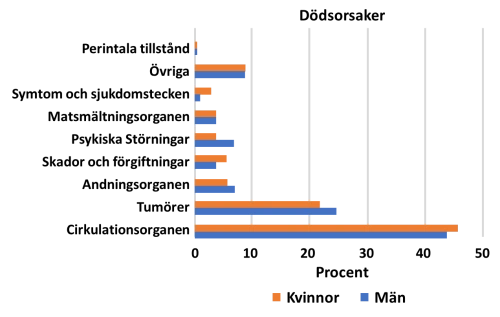
Vi utgår från diagrammet och lokaliserar staplarna för kvinnor som har orange färg. Sjukdomar i cirkulationsorganen står för cirka 45% och sjukdomar i matsmältningsorganen för cirka 3%. Kvoten mellan 45% och 3% är $\frac{45}{3}$ = 15.
Svar: Tre gånger fler kvinnor dog pga. sjukdomar i cirkulationsorganen än av sjukdomar i matsmältningsorganen.Ytdiagrammen (även kallat areadiagram) förkommer i högskoleprovuppgifter där det är viktigt att analysera både totalen och de ingående delarna samt att kunna identifiera trender, ofta över tid.
Diagrammet visar volymen råvaror som transporterades i internationell sjöburen handel 1975–94 fördelad på råvarugrupper. Miljoner ton. Hur stor var den sammanlagda volymen råolja och oljeprodukter jämfört med volymen järnmalm som transporterades 1990?
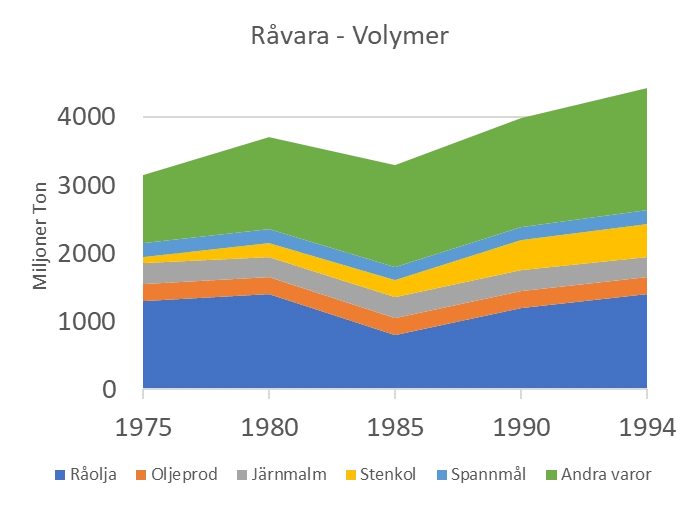
Vi utgår från året 1990 och börjar med att ta reda på volymen råolja, oljeprodukter och järnmalm enligt förklaringen under diagrammet. Avläsning ger:
Totala volymen råolja och oljeprodukter i förhållande till järnmalm är $\frac{1200+200}{350}$ = 4 gånger.
Svar: Råolja och oljeprodukter stod för fyra gånger större volym jämfört med järnmalm.Flödesdiagram förekommer ibland i uppgifter på Högskoleprovet. Till skillnad från övriga diagram beskrivna ser nästan alla flödesdiagram olika ut. Gemensamt är att diagrammen visualiserar beroenden mellan olika aktiviteter eller resurser och att det ofta finns en tidsparameter. Exempelvis visualisering av olika produktionssteg i en fabrik, råvaruförädling och flödet av varans väg från råvara till färdig produkt, etc.
Hur stor andel av sågtimret blev flis?
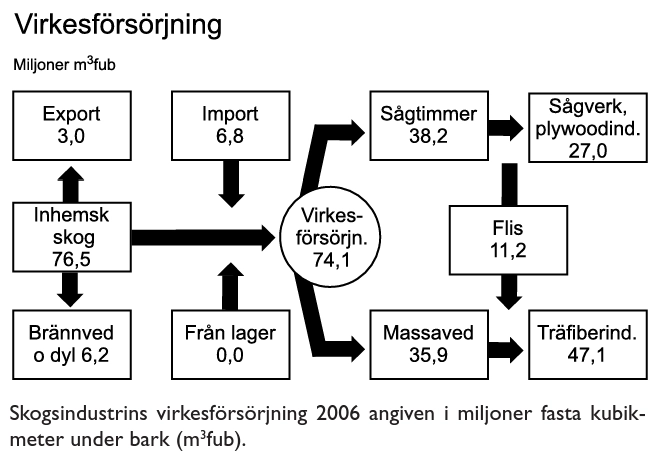
Vi utgår från diagrammet och rektangeln Sågtimmer $38,2\,m^3.$ Vi ser att sågtimmer delas upp i två delar: Flis $11,2\,m^3$ och Sågverk, plywoodind. $27,0\,m^3.$
Andelen flis är alltså $\frac{11,2\,m^3}{38,2\,m^3}\approx\frac{12}{36}=\frac13$
Svar: Andelen flis är cirka $30\text{%.}$Kombinationsdiagram används i uppgifter då man vill visualisera ytterligare information i ett och samma diagram. I vissa uppgifter förekommer två linjära axlar och vi behöver då vara noggranna att läsa av rätt axel.
Diagrammen visar månadsnederbörd i Karlstad och Vänersborg samt vattenföring i Göta älv och Klarälven, åren 1910 och 2000. Nederbörd i millimeter, vattenföring i kubikmeter per sekund (m3/s).

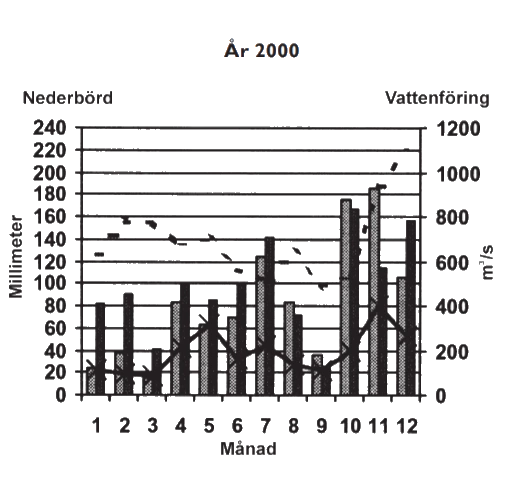
För uppgiften a ska vi jämföra de två diagrammen och ta reda på skillnaden av Klarälvens högsta och lägsta vattenföring för respektive år. Enligt förklaringen ser vi att vi ska använda oss av den heldragna linjen. Vi ska läsa av värdena på den högra vertikala skalan med enheten m3/s.
För året 1900 läser vi av diagrammet och noterar att den högsta vattenföringen skedde i månad 5 (maj) med cirka 520 m3/s. och den lägsta i månad 1 eller månad 12 med ca. 20 m3/s. Skillnaden är således cirka 520 - 20 = 500 m3/s.
För året 2000 finner vi det högsta noteringen i månad 11 med cirka 400 m3/s och den lägsta i månad 1, 2, 3 och 9 med cirka 100 m3/s. Skillnaden är cirka 400 - 100 m3/s.
För uppgift b klarar vi oss med enbart det övre diagrammet (för 1910). Uppgiften består i att beräkna andelen nederbörd som föll i Karlstad under april - juni (månad 4, 5, 6) i förhållande till hela året. Förklaringen ger oss att Karlstad representeras av den grå stapeln och det är den vänstra vertikala skalan med enheten mm.
Vi läser av diagrammet och noterar nederbörden för respektive månad:
1. 60 mm. 2. 50 mm. 3. 0 mm. 4. 55 mm. 5. 60 mm. 6. 45 mm. 7. 130 mm. 8. 45 mm. 9. 55 mm. 10. 60 mm. 11. 120 mm. 12. 45 mm.
Andelen nederbörd i april - juni 1910 =
$\large{\frac{55+60+45}{60+50+20+55+60+45+130+45+55+60+120+45}=}$
$\large{=\frac{160}{745}}\approx\frac{160}{800}=$ 0,2 = 20%.
Svar: a. 500 m3/s respektive 300 m3/s. b. 20%.