

Den allmänna potensfunktionen kan skrivas som: $$f(x)=ax^{n}$$ där $a$ och $n$ är konstanter, och $x$ är den oberoende variabeln som återfinns i potensens bas. Om $n = 0$ eller $n = 1$, så är funktionen en linjär funktion och får då en linjär graf. Detta eftersom $x^0= 1$ och $x^1 = x$.
Om vi ritar funktionen $f(x) = x^{2}+8x+7=0$ i en graf får vi följande:
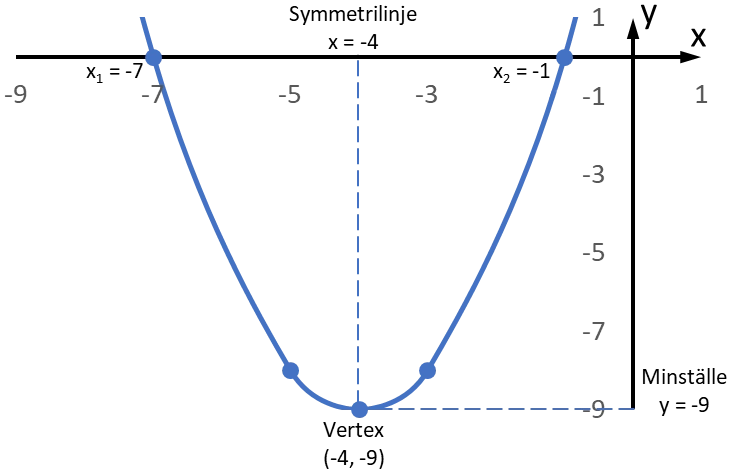
En potensfunktion vars graf ser ut så här kallas för en parabel. I vårt fall har vi markerat våra två rötter $x_1 = -1$, $x_2 = -7$. Dessa kallas nollställen. Vårt a-värde från pq-formeln är större än 0 och då vet vi att kurvan är konkav och har en "glad mun". Om a-värdet är negativt får vi en konvex kurva och en "ledsen mun".
Konkava kurvor har en minimipunkt eller även kallat maxställe och konvexa kurvor har en maximipunkt eller maxställe. Samlingsnamnet för en kurvas minimipunkt eller maximipunkt är extrempunkt. För att beräkna extrempunkten för en funktion med två rötter beräknar vi funktionens symmetrilinje, vilket är lika med medelvärdet av kurvans rötter. I vårt fall är kurvans symmetrilinje
$x=\frac{x_1+x_2}{2}=\frac{-7 + -1}{2}=-4$
Sätter vi in $x = -4$ i vår funktion får vi:
$f(-4)={-4}^2+8\cdot-4+7= -9$.
Vår funktions minsta värde är $-9$. Punkten $(-4, -9)$ är koordinaterna för funktions minimipunkt och kallas för vertex.
$f(x) = -x^2 + 2x + 3$. Bestäm funktionens nollställen, största värde och vertex.
Vi börjar med att bestämma nollställena genom pq-formeln:
$p=\frac ba=\frac {2}{-1}=-2$ och $q=\frac ca=\frac {3}{-1}=-3$
insatt i pq-formeln ger detta:
$x=-\frac{p}{2}\pm\sqrt{\left (\frac{p}{2} \right )^{2}-q}=$
=$-\frac{-2}{2}\pm\sqrt{\left (\frac{-2}{2} \right )^{2}+3}=1\pm\sqrt4=1\pm2$
$x_1= 3$, $x_2 = -1$
Symmetrilinjen ges av medelvärdet av nollställena, dvs $x=\frac{3 + -1}{2}=1$
För att bestämma funktionens största värde beräknar vi $f(1) = -1 + 2 + 3 = 4$.
Funktionens största värde är $4$ och vertex är $(1, 4)$.
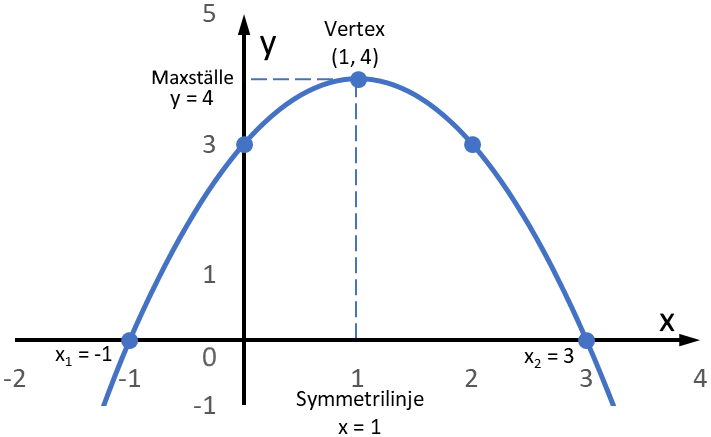
Svar: Funktionens nollställen är $x_1= 3$, $x_2 = -1$. Största värde är $y = 4$ och vertex är punkten $(1, 4)$.
En fotbollsmålvakt kastar ut bollen. Kastet är en parabel och kan beskrivas med funktionen $y(x)=-\frac{x^2}{4}+5x$ där $y$ är bollens höjd och $x$ är längden på kastet. Vad är bollens högsta höjd?
Vi börjar med att bestämma nollställena. Då vi inte har en konstant i vår funktion kan vi enkelt faktorisera:
$y(x)=-\frac{x^2}{4}+5x=x(-\frac{x}{4}+5)$
Den ena roten får vi om vi sätter det som står utanför parentesten lika med noll, dvs $x_1=0$ och den andra roten om vi sätter det innanför parentesten lika med noll, dvs $-\frac{x}{4}+5=0$ vilket ger $x_2=20.$
Vi vet att funktionen är konvex (termen $x^2$ är negativ) och därmed har vi en maximipunkt. Vi vet också att funktionen är symmetrisk kring maximipunkten och med våra två rötter beräknar vi symmetrilinjen $=\frac{x_1+x_2}{2}=\frac{0+20}{2}=10.$ Högsta höjden nås alltså efter kastlängden $10\,m$ och vi bestämmer höjden:
$f(10)=-\frac{10^2}{4}+5\cdot 10=25\,m$
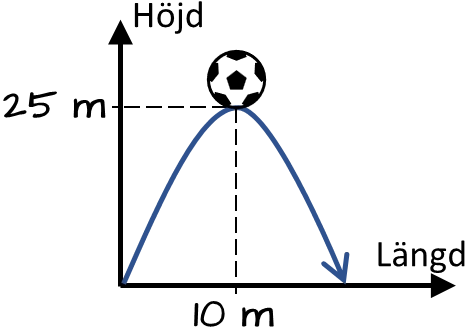
Svar: Högsta höjden på bollen är $25\,m.$
Den allmänna exponentialfunktionen kan beskrivas av funktionen: $$f(x)=C\cdot a^{x}$$ där $C$ och $a$ är konstanter, och x är den oberoende variabeln som återfinns i potensens exponent.
Följande exempel är hämtat från Högskoleprovet våren 2012 och visar karaktären på exponentialkurvor beroende på värdena C och a.
A. $y = -100 \cdot 0,7^x$



En bakteriekultur fördubblas varje timme. Från början finns 100 bakterier.
A. Hur många bakterier finns det efter 1, 2 och 3 timmar?
B. Skriv en formel för antalet bakterier efter $\boldsymbol{t}$ timmar.
Vi har en startpopulation med $C=100$ bakterier som fördubblas varje timma, dvs tillväxtfaktorn $a=2.$.
Antalet bakterier efter 1, 2, 3 timmar:
Varje timma har vi alltså en fördubbling av antalet bakterier och vi kan skriva detta som $C\cdot2^t$ där $C=100$ är antalet bakterier från början och tillväxtfatorn $a=2$ och $t$ är antalet timmar som gått sedan vi började mäta.
Ett radioaktivt ämne halveras varje dag. Från början finns 80 gram.
A. Hur mycket finns kvar av ämnet efter 1, 2 och 3 dagar?
B. Skriv en formel för massan efter $\boldsymbol{t}$ dagar.
Vi har en startmassa med $C=80$ gram som halveras varje dag och då vet vi att halveringsfaktorn är $a=0,5$:
Massan efter 1, 2, 3 dagar:
Varje dag har vi alltså en halvering av massan och vi kan skriva detta som $C\cdot 0,5^t$ där $C=80\,g$ är massan från början och halveringsfaktorn $a=0,5$ och $t$ är antalet dagar som gått sedan vi började mäta.
En bakteriekultur växer enligt formeln $N(t)=C \cdot a^t$ där $N(t)$ är antalet bakterier efter $t$ timmar, $C$ är startantalet bakterier och $a$ är tillväxtfaktorn. Efter tre timmar finns det $200$ bakterier, och tillväxtfaktorn är $a=2.$
Bestäm $C.$
Vi sätter in värdena som vi får givna i uppgiften: $N(t)=C \cdot 2^3.$
$200=C\cdot 8 \Rightarrow C=\frac{200}{8}=\frac{200/8}{8/8}=25.$
Svar: $C=25.$