

Uttryck där båda leden inte är lika stora kallas för olikheter. De tecken som används för olikheter är:
$2x + 5 \lt 3$. Vad är $\boldsymbol{x?}$
Det här uttrycket läser vi som att två $x$ + fem är mindre än tre. Uttrycket löser vi på samma sätt som om olikhetsteckenet hade varit ett likamedtecken. Vi börjar med att samla våra obekanta, dvs $2x,$ i vänsterledet och konstanter, dvs $5$ och $3,$ i högerledet:
$2x \lt 3 - 5$
$2x \lt -2$
Därefter dividerar vi båda leden med två för att få $x$ ensamt i högerledet:
$x \lt \frac{-2}{2}$
$x \lt -1$.
Vi ritar olikheten på tallinjen enligt ovan.
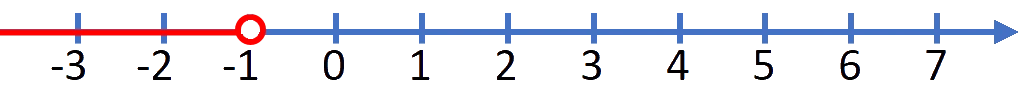
$\frac35-x\ge \frac25x-\frac25.$ Vad är $\boldsymbol{x?}$
$\frac{3+2}{5}\ge \frac{2+5}{5} x$
$1 \ge \frac75 x$
$\frac57 \ge x$
Svar: $x \le \frac57$Kalles företag säljer kickbikes. Priset för en kickbike är 3,000 kr, Kalles fasta kostnader är 80,000 kr per år och han har en marginal på 20% för varje såld kickbike. Hur många kickbikes måste han minst sälja för att göra en vinst (försäljning minus kostnader) på 400,000 kr per år?

Det här är en olikhet där Kalles vinst ska vara större än eller lika med 400,000 kr. Vi kallar antalet kickbikes han säljer $x$ och försäljningen är $3000x.$ Han har en fast kostnad på $80000$ kr.
Marginalen räknar vi som $\frac{pris-kostnad}{pris}=0,2.$
För varje kickbike har han alltså vinsten (pris - kostnad) $=3000 \cdot 0,2.$ Det här ger oss:
$(3000\cdot0,2)x - 80,000 \ge 400000$
$(3000\cdot 0,2)x \ge 480000$
$x \ge \frac{480000}{3000\cdot0,2}=\frac{480000}{600}=800$
Svar: Kalle behöver minst sälja 800 kickbikes.Det finns en viktig regel som skiljer ekvationslösning med olikheter från ekvationslöning där inte olikheter förekommer, dvs där vi har likhetstecken i ekvationen: Olikhetstecken ska vändas om multiplikation eller division med negativa tal.
Vilket svarsförslag ger alla lösningar till olikheten $\boldsymbol{3 – 2x \lt 1?}$
För att få $x$ positivt multiplicerar vi bägge sidor med $-1.$ Som vi förklarat gäller att olikhetstecknet ska vändas om multiplikation eller division med negativt tal, dvs.
$-1(3 - 2x \lt 1)$ Detta ger:
$-3 + 2x \gt -1$ och $2x \gt 2$ och slutligen $x \gt 1$.
Svar: $x \gt 1$.
Ett bra sätt att lösa olikheter är att rita en tallinje. Det är speciellt användbart för uppgifter med flera obekanta. Då vi ritar olikheten på tallinjen markerar vi att olikheten är öppen med en ring. Det betyder att x inte kan anta värdet (exempelvis x $\lt$ 1). En sluten olikhet och markeras med en ifylld ring (exempelvis x $\le$ 1).
$x + 5 \gt 7$ och $y – 3 \le -2$
Bestäm om $\boldsymbol{x}$ är större än $\boldsymbol{y}$, lika med $\boldsymbol{y}$ eller mindre än $\boldsymbol{y}$
Vi kallar våra giva olikheter 1 respektive 2:
Vi ritar våra två olikheter på tallinjen. Vi markerar talet ett med en ifylld ring, då $y$ är mindre än eller lika med ett. Samtidigt markerar vi talet två med en icke-ifylld ring då $x$ är större än två, men inte lika med två.

En olikhet på formen $–12 \le 2x + 6 \le 8$ kallar vi sammansatt olikhet. Det är ett uttryck som består av två olikheter och kan lösas genom att dela upp uttrycket i två olikheter och lösa dessa var och en för sig.
Lös $\boldsymbol{x}$ för olikheten $\boldsymbol{–12 \le 2x + 6 \le 8}$
Vi delar upp olikheten i två:
Olikhet 1: $–12 \le 2x + 6$
$-12 - 6 \le 2x$
$-18 \le 2x$
$\frac{-18}{2} \le \frac{2x}{2}$
$-9 \le x$
Olikhet 2: $2x + 6 \le 8$
$2x \le 8 - 6$
$2x \le 2$
$\frac{2x}{2} \le \frac{2}{2}$
$x \le 1$
Vi kan nu åter sätta ihop vår olikhet och får:
$-9 \le x \le 1$
