Medelvärde, median, typvärde och variationsbredd på Högskoleprovet

Linjära ekvationer Olikheter Procent och promille Talföljder Räta linjens ekvation Enheter och prefix Omkrets, area och volym Medelvärde, median… Tabeller

Andragradsekvationer Bråk och decimaler Räkneregler Funktioner Fyrhörningar Trianglar Sannolikhet Kartor

Ekvationer i bråkformat Potensregler Rötter Potens-/exponentialfunktioner Cirkeln Likformighet Vinklar och parallella linjer Diagram

Lär dig använda medelvärde, median, typvärde och variationsbredd på högskoleprovet. Vi går igenom vad de olika läges- och spridningsmåtten betyder, hur de beräknas och hur du använder dem för att lösa olika typer av uppgifter.

Sammanfattning Medelvärde, median, typvärde och variationsbredd på Högskoleprovet

Medelvärde (Eng. mean), median och typvärde (Eng. mode) är lägesmått som på olika sätt beskriver ett datamaterials centrala eller typiska värden.

Medelvärde = $\frac{\text{Summan av värdena}}{\text{Antal värden}}$
Medianen av ett udda antal tal är det mittersta talet om de ordnas i storleksordning.
Medianen av ett jämnt antal tal är medelvärdet av de två mittersta talen om de ordnas i storleksordning.
Typvärde är det tal som förekommer flest gånger.

Variationsbredd är ett spridningsmått som beskriver skillnaden mellan det största och minsta värdet.

Variationsbredd = Maxvärdet - Minvärdet

Lägesmått och spridningsmått

Medelvärde (Eng. mean), median och typvärde (Eng. mode) är exempel på så kallade lägesmått. Variationsbredd (Eng. range) är exempel på spridningsmått. Lägesmått beskriver på olika sätt ett datamaterials centrala eller typiska värden. Spridningsmått används för att beskriva hur stor skillnaden är mellan värden i ett urval och avståndet av medelvärdet och våra största respektive minsta värden.

I en symmetrisk normalfördelning sammanfaller medelvärde, median och typvärde. I ett skevt datamaterial påverkas medelvärdet mer av extrema värden, medan medianen ofta ger en bättre bild av datamaterialets centrala värde.

Datamaterial med sju värden som illustrerar medelvärde, median, typvärde och variationsbredd

För att beskriva urvalet av de sju värdena ovan bestämmer vi tre lägesmått och ett spridningsmått:

Medelvärde $=\frac{1+1+1+2+2+3+11}{7}=3$
Median vid ett ojämnt antal tal $=$ det mittersta värdet $=2$
Typvärdet $=$ det vanligaste värdet $=1$
Variationsbredd $=$ differensen mellan det största värdet och det minsta värdet $=11-1=10$

Medelvärde

Medelvärdet är ett lägesmått som beskriver det genomsnittliga värdet i ett datamaterial. Medelvärdet beräknas genom att summera alla värden och dividera summan med antalet värden.

$$medelvärde = \frac{summan\;av\; värdena}{antal \, värden}$$

Median

Ibland är medelvärdet ett dåligt mått och medianen fungerar bättre. Medianen är det värde för ett ordnat datamaterial som delar materialet i två lika stora delar. Kom ihåg: Värdena måste först ordnas i storleksordning innan medianen bestäms.

Medianen av ett udda antal tal =
Det mittersta talet om de ordnas i storleksordning.

Medianen av ett jämnt antal tal =
Medelvärdet av de två mittersta talen om de ordnas i storleksordning.

Typvärde

Typvärde (Eng. mode) är ett lägesmått på samma sätt som medelvärde och median. Typvärdet är det värde som förekommer flest gånger i dataserien.

Typvärde = Det värde som förekommer flest gånger

Om alla värden i dataserien är olika finns inget typvärde (typvärde saknas).
Om två eller fler värden förekommer oftare än andra värden finns flera typvärden.

En dataserie med två typvärden kallas bimodal.
En dataserie med tre typvärden kallas trimodal.
En dataserie med fler än tre typvärden kallas multimodal.

Variationsbredd

Variationsbredd, Vb (Eng. range) är ett spridningsmått som ger oss en uppfattning om hur stora skillnader (spridning) det är i vårt informationsmaterial.

Variationsbredd (Vb) = Maxvärdet - Minvärdet

Exempel: Medelvärde, Median, Typvärde och Variationsbredd

Kalle mätte nederbörden under en vecka. Vad är medelvärdet, medianen, typvärdet och variationsbredden av nederbörd per dag?

Dag	Nederbörd
Måndag	6 mm
Tisdag	17 mm
Onsdag	6 mm
Torsdag	6 mm
Fredag	2 mm
Lördag	7 mm
Söndag	12 mm

Medelvärde $= \frac{summan\;av\; värdena}{antal \, värden}=$
$=\large{\frac{(6+17+6+6+2+7+12)\; mm}{7\;dagar}}$ $=\frac{56}{7}=8\, mm/dag.$
För att bestämma medianen behöver vi sortera våra värden enligt storleksordning:
${2, 6, 6, 6, 7, 12, 17}$
Medianen = Det mittersta av talen (tal nummer fyra i serien) $= 6\, mm.$
Typvärdet är det värde som förekommer flest gånger, dvs $6\, mm$ (vid tre tillfällen).
Variationsbredden $=$ Maxvärdet $-$ Minvärdet $= (17 - 2)\, mm = 15\, mm.$

Svar: Medelvärdet $= 8\, mm,$ medianen $= 6\, mm,$ typvärdet $= 6\, mm$ och variationsbredden $= 15\, mm.$

Exempel: Medelvärde, Median, Typvärde och Variationsbredd 2

På vårterminen hade klassen fem prov. Medelvärdet på de tre första proven var $70$ poäng och på alla fem proven $80$ poäng. Vad var medelvärdet på prov fyra och fem?

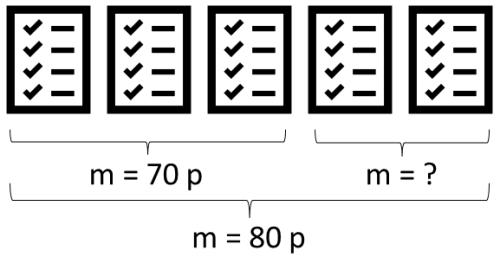
Fem provresultat där medelvärdet för de tre första och alla fem proven är känt

Vi betecknar poängen på de fem proven med $p1, p2, p3, p4$ och $p5.$ Vi söker medelvärdet av prov fyra och fem, dvs $\frac{p4+p5}{2}$

Medelvärdet på de tre första proven kan vi skriva $\frac{p1+p2+p3}{3}=70\,p$ och medelvärdet på alla fem proven $\frac{p1+p2+p3+p4+p5}{5}=80\,p$

Därmed kan vi skriva $\frac{p4+p5}{2}=\frac{5\cdot 80 - 3\cdot70}{2}=\frac{190}{2} = 95\, p.$

Svar: Medelvärdet på prov fyra och fem är $95\, p.$

Exempel: Medelvärde, Median, Typvärde och Variationsbredd 3

En klass med $x$ elever fick medelvärdet $20\, p$ på ett prov och en klass med $y$ elever fick $28\, p$ på samma prov. Tillsammans fick de två klasserna provmedelvärdet $22\, p.$ Vad är $\boldsymbol{\frac{x}{y}?}$

Två klasser med olika antal elever och olika medelvärden på samma prov

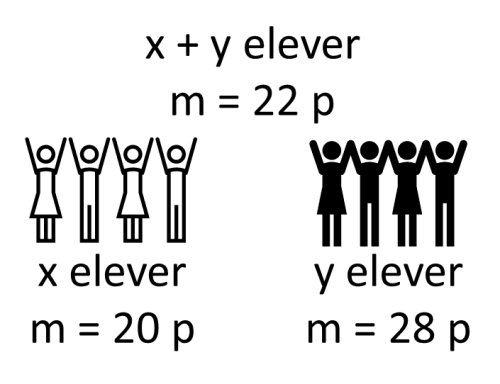
Vi kallar summan av klassernas provresultat $A$ respektive $B.$

I texten får vi tre ekvationer:

$\frac{A}{x}=20\,p.$
$\frac{B}{y}=28\,p.$
$\frac{A+B}{x+y}=22\, p.$

Ekvation ett ger $A = 20x$ och ekvation två ger $B = 28y$

Ekvation ett och två insatt i tre ger: $\frac{20x + 28y}{x+y}=22$

$20x + 28y = 22x + 22y$

$6y=2x \Rightarrow \frac{x}{y}=3$

Svar: $\frac{x}{y}=3$

Exempel: Medelvärde, Median, Typvärde och Variationsbredd 4

Medelvärdet av fyra tal är $14$ med variationsbredden $20.$ Det största talet tas bort. Variationsbredden är nu noll. Vilket tal togs bort?

Variationsbredden noll säger oss att talen som är kvar är lika stora. Kalla vart och ett av de tre lika talen $x$ och det borttagna största talet $y.$

$\frac{3x+y}{4}=14$
$y-x=20$

Ekvation ett ger: $3x+y=56$

Ekvation två ger: $y=x+20$

Insättning:

$3x+x+20=56 \Rightarrow x=\frac{56-20}{4}=9$

$y=56- 3\cdot9 = 56 - 27 = 29$

Svar: Talet $29$ togs bort.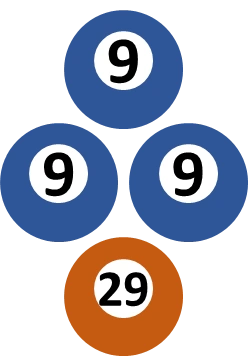

medelvärde4

Exempel: Medelvärde, Median, Typvärde och Variationsbredd 5

I en kortgiv är medelvärdet av de första fyra korten $4$ och typvärdet är $2.$ Då ett femte kort dras ändras typvärdet till $2$ och $4.$ Vilka är korten?

Fem kort som används för att bestämma medelvärde och typvärde

Eftersom typvärdet för de fyra första korten är $2$ måste talet $2$ förekomma oftare än de andra värdena. Det innebär att minst två av korten är tvåor.

Det femte kortet måste vara en fyra eftersom vi nu har två typvärden: $2$ och $4.$ Kvar att bestämma är det okända kortet som vi kallar $x:.$

Med hjälp av medelvärdet av de fyra första korten beräknar vi $x:$

$\frac{2+2+4+x}{4}=4$

$2+2+4+x=16$

$x=16-(2+2+4)=8$

Svar: Korten är $2, 2, 4, 8, 4$