Linjära ekvationer (Förstagradsekvationer) på Högskoleprovet

Sammanfattning Linjära ekvationer (Förstagradsekvationer) på Högskoleprovet

Linjära ekvationer med en obekant löser vi genom att successivt utföra räkneoperationer på båda leden samtidigt till vi får den obekanta ensamt i det ena ledet.
Förstagradsekvationer med fler än en obekanta löser vi med grafisk lösning, substitutionsmetoden eller additionsmetoden.
Grafisk lösning får vi om vi ritar kurvorna av våra ekvationer i ett koordinatsystem. Kurvornas skärningspunkt är lösningen till ekvationssystemet.
Med substitutionsmetoden ersätter vi en av de obekanta med ett uttryck av den andra obekanta.
Med additionsmetoden adderas ekvationerna så att någon av de obekanta försvinner.
Ett ekvationssystems lösbarhet beror på:

Lika många ekvationer som obekanta.
Ekvationerna är linjärt oberoende.

Med ett venndiagram kan vi strukturera information för bättre överskådlighet och snabbare lösa ekvationer med likheter och olikheter.

Ekvationer med enbart en obekant

Ekvationer med enbart en obekant löser vi genom att utföra räkneoperationer på båda leden samtidigt. Steg för steg förenklar vi ekvationen till att vi får den obekanta ensamt i det ena ledet.

Exempel: Ekvationslösning med en obekant

3x - 7 = 2. Bestäm x.

Vi börjar med att addera 7 i båda leden:
3x - 7 + 7 = 2 + 7
3x = 9
Därefter dividerar vi båda led med 3:
$\frac{3x}{3}=\frac93$
x = 3

Svar: x = 3

Exempel: Ekvationslösning med en obekant 2

Klara är 26 år och hennes dotter är 4 år. Om hur många år är Klara dubbelt så gammal som sin dotter?

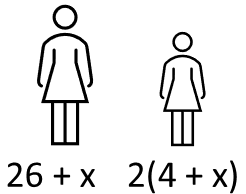
ekvationer

Vi kallar antal år till Klara är dubbelt s få gammal som sin dotter x och skriver det vi får initialt i uppgiften som en ekvation:

Om x år är Klara 26 + x år och hennes dotter är 4 + x år. Vi söker x så att Klaras ålder + x år = 2 (dubbelt) gånger hennes dotters ålder:
$26+x=2(4+x)$
$26+x=8+2x$
$x=18$

Om 18 år är Klara $26 + 18=44$ år och hennes dotter är $4 + 18=22$ år.

Svar: Om 18 år.

Ekvationer med fler obekanta

Förstagradsekvationer med fler än en obekanta löser vi med någon av följande tre metoder:

Grafisk lösning
Substitutionsmetoden
Additionsmetoden

Att lära sig att lösa linjära ekvationer med de olika metoderna kan spara tid på Högskoleprovet.

Grafisk lösning

Med denna metod ritar vi linjerna av de två ekvationerna i syfte att bestämma var de möts (skär varandra). Denna punkt kallar vi skärningspunkt. Skärningspunktens x- respektive y-värde ger oss lösningen på ekvationerna.

Exempel: Grafisk lösning

y = 2x - 3 och y = x - 2. Bestäm x och y.

Vi ritar vår två ekvationer i en graf enligt nedan. Linjernas skärningspunkt ger oss svaret på uppgiften.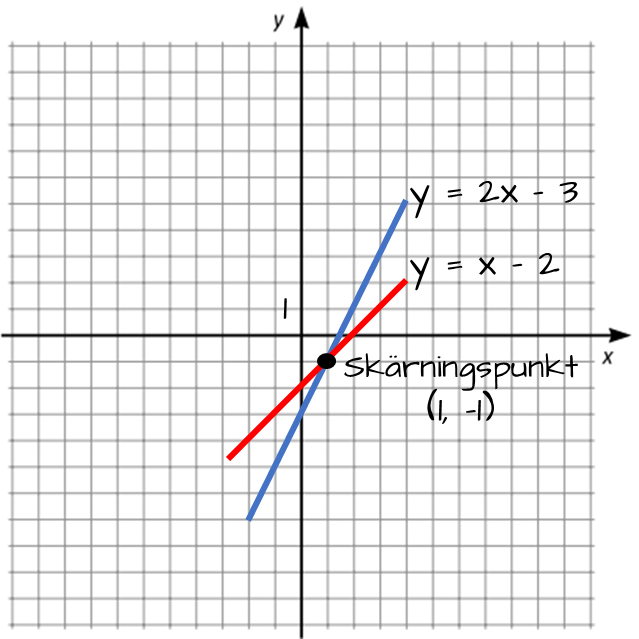

linjers-skärningspunkt

Svar: x = 1, y = -1.

Substitutionsmetoden

Med substitutionsmetoden löser vi ut en av våra obekanta ur en ekvation och ersätter det uttryck vi får fram i den andra ekvationen.

Exempel: Substitutionsmetoden 1

Bestäm x och y med hjälp av de två ekvationerna nedan:

y - 4 = 2x
x + y = 4x + 2

Ekvation 1: y - 4 = 2x vilket ger att y = 2x + 4

Ekvation 2: Vi ersätter y med 2x + 4:
x + (2x + 4) = 4x + 2
vilket ger 4 - 2 = 4 x - 3x och x = 2
x = 2 insatt i ekvation 1 ger: y = 2 · 2 + 4 = 8.

Svar: x = 2, y = 8.

Exempel: Substitutionsmetoden 2

Claras och Alicias sammanlagda längd är 3,20 m. Alicias och Bedas sammanlagda längd är 3,30 m. Den sammanlagda längden för alla tre är 4,80 m. Hur lång är Alicia?

Kalla Alicias längd A
Kalla Bedas längd B
Kalla Claras längd C

Vi får veta att

C + A = 3,20 m
A + B = 3,30 m
A + B + C = 4,80 m

Vi har tre obekanta: A, B och C och tre ekvationer: 1, 2 och 3.

Ekvation 1 ger at A = 3,2 - C

Ekvation 2 ger att B = 3,3 - A

Ekvation 1 och 2 insatt i 3 ger:

(3,2 - C) + (3,3 - A) + C = 4,8=

6,5 - A = 4,8 vilket ger att A = Alicias längd = 1,7 m.

Svar: Alicia är 1,7 m.

Additionsmetoden

Additionsmetoden innebär att vi adderar ekvationerna så att någon av de obekanta försvinner. Ibland behöver vi multiplicera ekvationerna med ett tal, om det inte är så att vi kan summera direkt.

Exempel: Additionsmetoden

Bestäm x och y med hjälp av de två ekvationerna nedan:

2y - 8 = -4x
y + 4 = 4x + 2

Ekvation 1 + Ekvation 2 ger:
2y - 8 + (y + 4) = -4x + (4x + 2)
3y - 4 = 2
3y = 6
vilket ger att y = 2.

Ekvation 1: y = 2 insatt i ekvation 1 ger:
2 · 2 - 8 = -4x vilket ger 4 - 8 = -4x och 4x = 4 dvs x = 1.

Svar: x = 1, y = 2

Ekvationssystems lösbarhet

Villkoren för att en ekvation ska vara lösbar är:

Antalet ekvationer måste vara lika många som antalet obekanta
Ekvationerna måste vara linjärt oberoende

Att en ekvation är linjärt oberoende betyder att den inte går att uttrycka som en av våra andra ekvationer. Vi visar vad vi menar med detta i exemplet nedan.

Exempel: Ekvationers Lösbarhet:

Bestäm x och y där $y = 2x - 2$ och $x =\frac{y}{2}+1$

Vi har två obekanta, x och y, och två ekvationer så det borde gå att lösa x och y. Vi provar med substitutionsmetoden:
Kalla ekvationerna 1 och 2:

$y = 2x - 2$
$x =\frac{y}{2}+1$

Ekvation 2 insatt i ekvation 1 ger:
$y = 2(\frac{y}{2}+1) - 2 = (y + 2) - 2 = y$

Genom substitutionsmetoden får vi att y = y och därmed är inte uppgiften i exemplet lösbar.
Villkoret att vi har lika många obekanta (x och y) som ekvationer (1 och 2) är uppfyllt, men ekvationerna är inte linjärt oberoende eftersom vi kan uttrycka ekvation 1 som ekvation 2 (och vice-versa).

Det här ser vi ännu tydligare om vi i ekvation 2 först multiplicerar vänsterledet och högerledet med 2 och därefter flyttar konstanten till vänsterledet:
$x =\frac{y}{2}+1$ Multiplicera båda led med 2:
$2x = y+2$ Flytta konstanten 2 till vänsterledet:
$y=2x-2$ Vilket är samma sak som ekvation 1.

Svar: Ekvationssystemet är inte linjärt oberoende och därmed inte lösbart.

Venndiagram

Ett Venndiagram är ett sätt att strukturera information som kan hjälpa dig att lösa ekvationer och olikheter snabbare på Högskoleprovet. Venndiagram har många praktiska tillämpningar och används bland annat för att ge överskådlighet av likheter och olikheter. För mer komplexa samband (fyra cirklar eller mer) minskar tydligheten.

Exempel: Venndiagram:

I klassen har 15 elever katt, 12 har hund, 5 elever har både katt och hund och 8 elever har inget husdjur. Hur många elever går i klassen?

venndiagram

Vi har ett förhållande mellan två variabler, dvs. hundar och katter, så vi ritar två cirklar. I den vänstra cirkeln fyller vi antalet elever som enbart har katt, dvs. 15 - 5 = 10 och i den högra cirkeln de som enbart har hund, dvs. 12 - 5 = 7.

I det fält som överlappar de två cirklarna, kallat snittet, fyller vi i antalet elever som har både katt och hund dvs. 5.

Slutligen fyller vi i antalet elever som inte har något husdjur, dvs. 8, utanför våra cirklar.

Då vi summerar våra tal får vi 10 + 5 + 7 + 8 = 30, vilket är totala antalet elever i klassen.

Svar: 30 elever går i klassen.