


Teorin är till största del samma på NOG som på XYZ och KVA. Här gäller att gå igenom de 25 mattekapitlen med exempel på AllaRätt.nu och Matematiken på Högskoleprovet.
Testa dig själv med de Interaktiva övningsprov på AllaRätt.nu är en utmärkt temperaturmätare på hur du ligger till och vad du behöver förbättra. På NOG så är en klar majoritet av uppgifterna inom algebra. Fördelningen av uppgifter och vilket matematikområde de tillhör finner du i grafen nedan.
Lösningsmetodiken för NOG utgår alltid efter att utveckla det som är givet så långt du kan:
Därefter applicerar du ett av de två påståenden åt gången. Svarsalternativen är fem och går ut på om uppgiften kan lösas av två påståenden (1 och 2).
Diagrammet nedan visar lösningsgången för NOG:
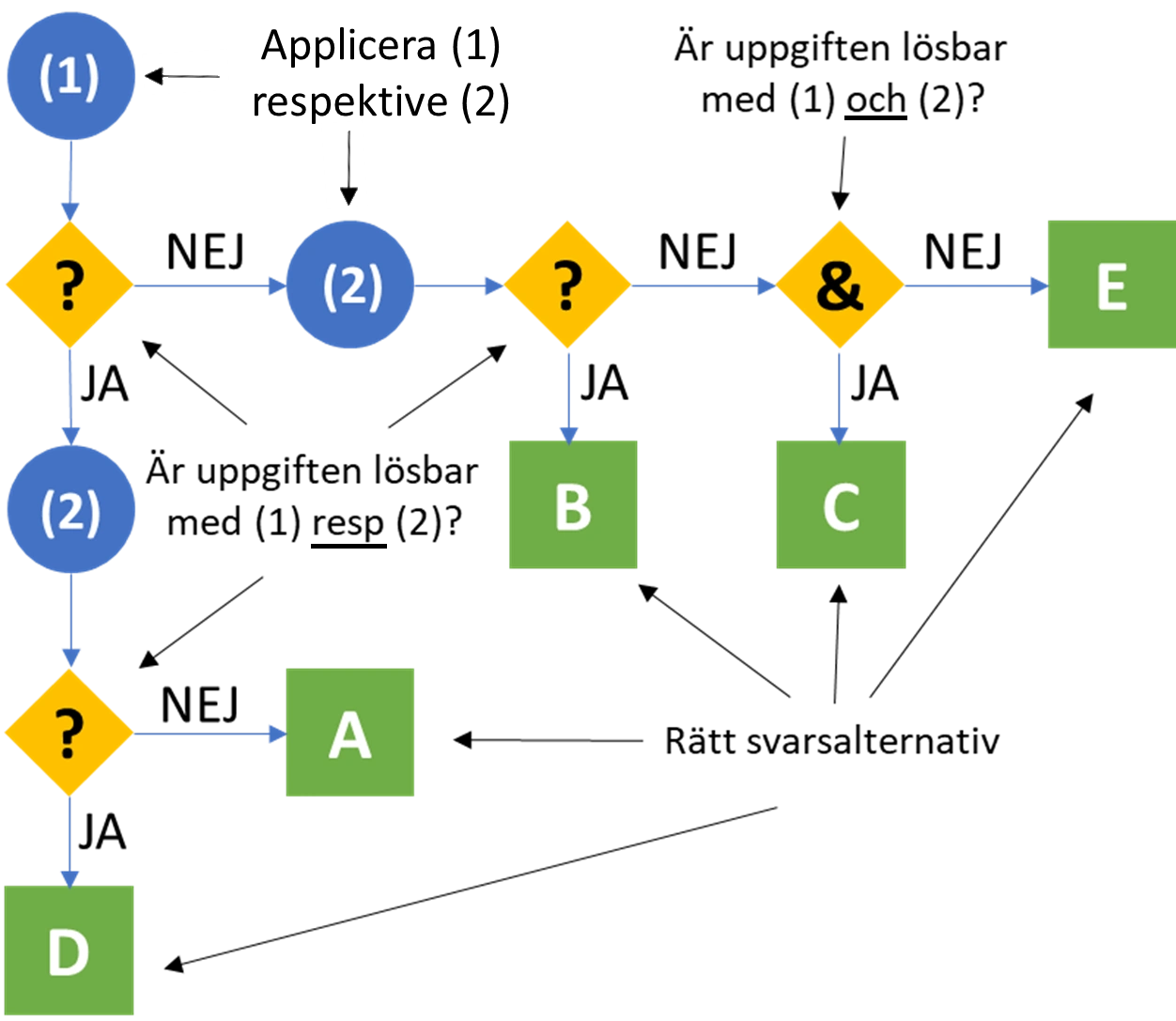
De som tycker att NOG är det mest utmanande delprovet på Högskoleprovet säger ofta att stressen är svårast och på NOG behöver du verkligen utnyttja tiden optimalt. På NOG är det särskilt viktigt att snåla med tiden, men det går också att öva upp din snabbhet. Kom ihåg att du bara behöver jobba med uppgiften till dess att du vet vad rätt svar är.
Märker du att en uppgift tar lång tid, lämna denna. Markera och återvänd då du är klar med de andra uppgifterna. Svarsalternativ C. (1) tillsammans med (2) är det vanligaste rätta svarsalternativet. Störst sannolikhet alltså, om du behöver chansa. På Om Högskoleprovet hittar du mer läsning om detta.

En viss typ av uppgifter förekommer enbart på NOG. På AllaRätt.nu hittar du dessa på Interaktiva övningsprov/NOG/Algebra/Olikheter. Här nedan visar vi ett exempel på detta.
En bofink, en domherre, en gråsparv och en talgoxe sitter på rad på en telefonledning. Bofinken sitter inte längst till höger. Vilken fågel sitter längst till vänster?
(1) Talgoxen sitter närmast till vänster om bofinken. Gråsparven sitter inte bredvid domherren.
(2) Talgoxen sitter inte bredvid gråsparven. Domherren sitter inte bredvid bofinken.
Initialt får vi veta att vi har fyra olika fåglar. Bofinken sitter inte längst till höger. Vi ska bestämma ordningen på fåglarna.
| (1) |
|
| (2) |
|
| Tillsammans | (1) och (2) tillsammans ger oss tillräcklig information för att lösa uppgiften och rätt svar är alltså C. |
 | |
Svar: Svarsalternativ C, (1) tillsammans med (2).
I uppgifter då det förekommer mycket information är rätt svarsalternativ oftast E (ej genom de båda påståenden). Speciellt i uppgifter då det gäller ekvationer så består vissa uppgifter av för mycket information eller irrelevant sådan. Dessa uppgifter är ofta olösbara. Misstänker vi att en uppgift är olösbar kan vi försöka hitta två alternativ som är motstridiga, vilket vi ger exempel på nedan:
Är $\boldsymbol{z < 0?}$
(1) $xz > yz$
(2) $xy > yz$
Vi får två olikheter och söker om $z < 0$
Då vi har tre obekanta $(x, y, z)$ och enbart två olikheter kan vi direkt dra slutsatsen att vi saknar information. För att vara säkra provar vi att först sätta $x = -1, y = 1$ och $z = -2.$ Detta uppfyller både (1) och (2) och $z < 0.$ Vi provar sedan att sätta $x = 3, y = 2$ och $z = 1.$ Detta uppfyller också (1) och (2), men $z$ är $> 0.$
Svarsalternativet E är således rätt.

Då vi utgår från vår statistik på AllaRätt.nu så är det svåraste området inom NOG uppgifter om Potensregler, uppgifter som berör Omkrets, area och Volym samt uppgifter om Trianglar. Listan nedan sammanställer andelen som besvarat uppgifter korrekt per område inom Högskoleprovets NOG:
Den svåraste NOG-uppgiften på Högskoleprovet sedan 2011 är en uppgift om ekvationer och som enbart 31% svarat rätt på. Uppgiften förekom på Högskoleprovet 2015, Vår provpass 2.
| Uppgift | % Rätt | År/Termin |
|---|---|---|
I en klass med 24 elever har hälften av pojkarna moped. Hur många flickor i klassen har moped? (1) Det är lika många flickor som pojkar i klassen. 14 elever har inte moped. (2) Av dem som inte har moped är flickorna 2 fler än pojkarna. Av flickorna är de som inte har moped 4 fler än de som har moped. Tillräcklig information för lösningen erhålls | 31% | 2015, Vår |
I två lådor finns det 67 bollar, 11 gröna och resten röda. I låda A finns det 7 gröna bollar. Hur många röda bollar finns det i låda B? (1) I låda A finns det tre gånger så många röda bollar som gröna bollar. (2) I låda B finns det 11 bollar fler än i låda A. Tillräcklig information för lösningen erhålls | 38% | 2016, Höst |
På en cirkus är antalet clowner 60 procent av antalet akrobater. Hur många akrobater finns det på cirkusen? (1) Om det hade funnits dubbelt så många clowner och hälften så många akrobater, så hade det funnits 7 fler clowner än akrobater på cirkusen. (2) Det finns 4 fler akrobater än clowner på cirkusen. Tillräcklig information för lösningen erhålls | 41% | 2025, Vår |
Bo ställer sig sist i en kö för att åka berg- och dalbana. Efter 10 minuter står det 100 personer i kön. Hur många personer står före Bo i kön vid denna tidpunkt? (1) Sedan Bo ställde sig i kön har antalet personer före honom i kön minskat med 55. (2) Sedan Bo ställde sig i kön har antalet personer efter honom i kön ökat med 36. Tillräcklig information för lösningen erhålls | 42% | 2022, Vår, Mars |
De fem bokstäverna A, B, C, D och E är skrivna på rad på ett papper. I vilken ordning från vänster till höger är bokstäverna skrivna? (1) D står längst till vänster. B står intill både C och E. A står längst till höger. (2) Varken D eller E står längst till höger. C står intill både A och B. B står intill både C och E. Tillräcklig information för lösningen erhålls | 42% | 2022, Höst |